Page 368 - Fiber Fracture

350 J.W.S. Hearle

0.1 5

X
g 0.10
- .-
r
u
E
0.05
i?

0 200 400 600 800 1000
Degree of polymerization

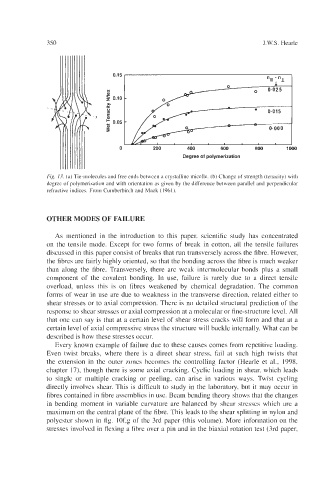
Fig. 13. (a) Tie-molecules and free ends between a crystalline micelle. (b) Change of strength (tenacity) with
degree of polymerisation and with orientation as given by the difference between parallel and perpendicular
refractive indices. From Cumberbirch and Mack (1961).

OTHER MODES OF FAILURE

As mentioned in the introduction to this paper, scientific study has concentrated
on the tensile mode. Except for two forms of break in cotton, all the tensile failures
discussed in this paper consist of breaks that run transversely across the fibre. However,
the fibres are fairly highly oriented, so that the bonding across the fibre is much weaker
than along the fibre. Transversely, there are weak intermolecular bonds plus a small
component of the covalent bonding. In use, failure is rarely due to a direct tensile
overload, unless this is on fibres weakened by chemical degradation. The common
forms of wear in use are due to weakness in the transverse direction, related either to
shear stresses or to axial compression. There is no detailed structural prediction of the
response to shear stresses or axial compression at a molecular or fine-structure level. All
that one can say is that at a certain level of shear stress cracks will form and that at a
certain level of axial compressive stress the structure will buckle internally. What can be
described is how these stresses occur.
Every known example of failure due to these causes comes from repetitive loading.
Even twist breaks, where there is a direct shear stress, fail at such high twists that
the extension in the outer zones becomes the controlling factor (Hearle et al., 1998,
chapter 17), though there is some axial cracking. Cyclic loading in shear, which leads
to single or multiple cracking or peeling, can arise in various ways. Twist cycling
directly involves shear. This is difficult to study in the laboratory, but it may occur in
fibres contained in fibre assemblies in use. Beam bending theory shows that the changes
in bending moment in variable curvature are balanced by shear stresses which are a
maximum on the central plane of the fibre. This leads to the shear splitting in nylon and
polyester shown in fig. lOf,g of the 3rd paper (this volume). More information on the
stresses involved in flexing a fibre over a pin and in the biaxial rotation test (3rd paper,