Page 114 - Fluid Mechanics and Thermodynamics of Turbomachinery

Axial-flow Turbines: Two-dimensional Theory 95
hence,

1
.h 2 h 3 / C .c y2 C c y3 /[.c y2 U/ .c y3 C U/] D 0.
2
It is observed from the velocity triangles of Figure 4.1 that c y2 U D w y2 ,c y3 C
U D w y3 and c y2 C c y3 D w y2 C w y3 . Thus,

2
1
.h 2 h 3 / C .w 2 w / D 0.
2 y2 y3
1 2
Add and subtract c to the above equation
2 x
1 2 1 2
h 2 C w D h 3 C w or h 02rel D h 03rel. (4.4)
2
3
2 2
2
1
Thus, we have proved that the relative stagnation enthalpy, h 0rel D h C w , remains
2
unchanged through the rotor of an axial turbomachine. It is implicitly assumed that
no radial shift of the streamlines occurs in this flow. In a radial flow machine a
more general analysis is necessary (see Chapter 7) which takes account of the blade
speed change between rotor inlet and outlet.
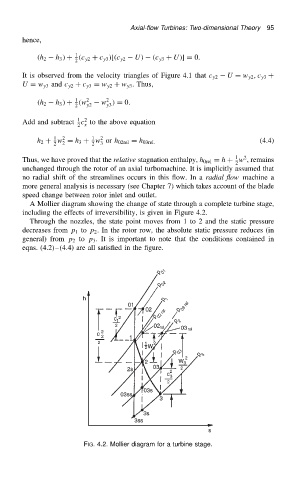
A Mollier diagram showing the change of state through a complete turbine stage,
including the effects of irreversibility, is given in Figure 4.2.
Through the nozzles, the state point moves from 1 to 2 and the static pressure
decreases from p 1 to p 2 . In the rotor row, the absolute static pressure reduces (in
general) from p 2 to p 3 . It is important to note that the conditions contained in
eqns. (4.2) (4.4) are all satisfied in the figure.

FIG. 4.2. Mollier diagram for a turbine stage.