Page 119 - Fluid Mechanics and Thermodynamics of Turbomachinery

100 Fluid Mechanics, Thermodynamics of Turbomachinery
at higher speeds. The axial velocity is limited by flow area considerations. It is
assumed that the blades are sufficiently short to treat the flow as two-dimensional.
The specific work done is

W D U.c y2 C c y3 /.
With W, U and c x fixed the only remaining parameter required to completely
define the velocity triangles is c y2 , since
c y3 D W/U c y2 . (4.16)

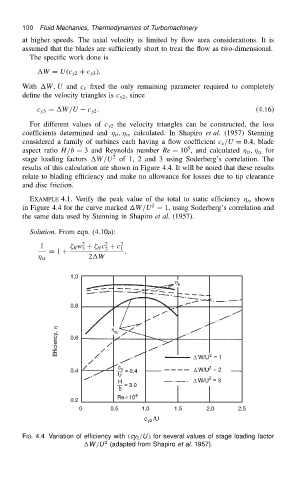
For different values of c y2 the velocity triangles can be constructed, the loss
coefficients determined and tt , ts calculated. In Shapiro et al. (1957) Stenning
considered a family of turbines each having a flow coefficient c x /U D 0.4, blade
5
aspect ratio H/b D 3 and Reynolds number Re D 10 , and calculated tt , ts for
2
stage loading factors W/U of 1, 2 and 3 using Soderberg’s correlation. The
results of this calculation are shown in Figure 4.4. It will be noted that these results
relate to blading efficiency and make no allowance for losses due to tip clearance
and disc friction.

EXAMPLE 4.1. Verify the peak value of the total to static efficiency ts shown
2
in Figure 4.4 for the curve marked W/U D 1, using Soderberg’s correlation and
the same data used by Stenning in Shapiro et al. (1957).
Solution. From eqn. (4.10a):
2
2
1 R w C N c C c 1 2
2
3
D 1 C .
ts 2W

FIG. 4.4. Variation of efficiency with .cy 2 /U / for several values of stage loading factor
2
W /U (adapted from Shapiro et al. 1957).