Page 77 - Fluid Mechanics and Thermodynamics of Turbomachinery

58 Fluid Mechanics, Thermodynamics of Turbomachinery
steady. The assumption of steady flow is valid for an isolated cascade row but, in a
turbomachine, relative motion between successive blade rows gives rise to unsteady
flow effects. As regards the assumption of incompressible flow, the majority of
cascade tests are conducted at fairly low Mach numbers (e.g. 0.3 on compressor
cascades) when compressibility effects are negligible. Various techniques are avail-
able for correlating incompressible and compressible cascades; a brief review is
given by Csanady (1964).
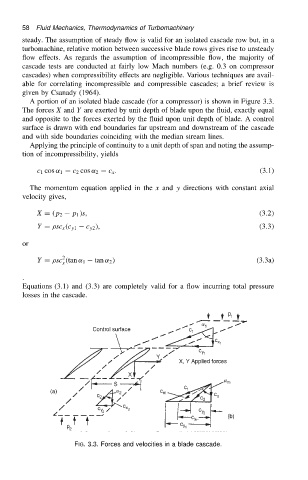
A portion of an isolated blade cascade (for a compressor) is shown in Figure 3.3.
The forces X and Y are exerted by unit depth of blade upon the fluid, exactly equal
and opposite to the forces exerted by the fluid upon unit depth of blade. A control
surface is drawn with end boundaries far upstream and downstream of the cascade
and with side boundaries coinciding with the median stream lines.
Applying the principle of continuity to a unit depth of span and noting the assump-
tion of incompressibility, yields
c 1 cos ˛ 1 D c 2 cos ˛ 2 D c x . (3.1)

The momentum equation applied in the x and y directions with constant axial
velocity gives,

p 1 /s, .3.2/
X D .p 2
c y2 /, .3.3/
Y D sc x .c y1
or

2
Y D sc .tan ˛ 1 tan ˛ 2 / (3.3a)
x
.
Equations (3.1) and (3.3) are completely valid for a flow incurring total pressure
losses in the cascade.

FIG. 3.3. Forces and velocities in a blade cascade.