Page 64 - Fluid Power Engineering

Hydraulic Oils and Theor etical Backgr ound 41

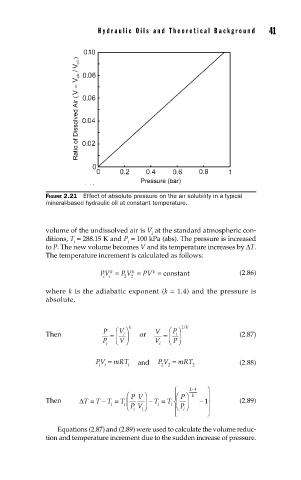
FIGURE 2.21 Effect of absolute pressure on the air solubility in a typical
mineral-based hydraulic oil at constant temperature.

volume of the undissolved air is V at the standard atmospheric con-
i
ditions, T = 288.15 K and P = 100 kPa (abs). The pressure is increased
i i
to P. The new volume becomes V and its temperature increases by ΔT.
The temperature increment is calculated as follows:
PV = P V = PV = constant (2.86)
k
k
k
ii 2 2
where k is the adiabatic exponent (k = 1.4) and the pressure is
absolute.

P ⎛ V ⎞ k V ⎛ P⎞ 1/ k
Then = ⎜ i ⎟ or = ⎜ ⎟ (2.87)
i
P ⎝ V ⎠ V ⎝ P ⎠
i i
PV = mRT and PV = mRT (2.88)
ii i 22 2

⎧ ⎧ k−1 ⎫
⎛ P V ⎞ ⎛ ⎪ P⎞ k ⎪
Then ΔT = T − T = T i ⎜ − T = T ⎨ − 1 ⎬ (2.89)
i ⎜ ⎟
⎝ P V ⎠ ⎪ ⎝ P ⎠ ⎪
i ⎟ i
i
i
i
⎩ ⎭
Equations (2.87) and (2.89) were used to calculate the volume reduc-
tion and temperature increment due to the sudden increase of pressure.