Page 156 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

138 SLENDER STRUCTURES AND AXIAL FLOW

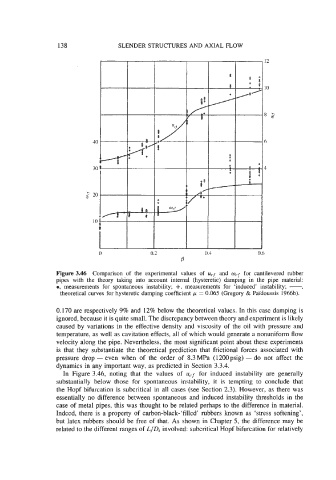
Figure 3.46 Comparison of the experimental values of ucf and wrf for cantilevered rubber
pipes with the theory taking into account internal (hysteretic) damping in the pipe material:
0, measurements for spontaneous instability; +, measurements for ‘induced’ instability; -,
theoretical curves for hysteretic damping coefficient p = 0.065 (Gregory & Pdidoussis 1966b).

0.170 are respectively 9% and 12% below the theoretical values. In this case damping is
ignored, because it is quite small. The discrepancy between theory and experiment is likely
caused by variations in the effective density and viscosity of the oil with pressure and
temperature, as well as cavitation effects, all of which would generate a nonuniform flow
velocity along the pipe. Nevertheless, the most significant point about these experiments
is that they substantiate the theoretical prediction that frictional forces associated with
pressure drop - even when of the order of 8.3 MPa (12OOpsig) - do not affect the
dynamics in any important way, as predicted in Section 3.3.4.
In Figure 3.46, noting that the values of ucf for induced instability are generally
substantially below those for spontaneous instability, it is tempting to conclude that
the Hopf bifurcation is subcritical in all cases (see Section 2.3). However, as there was
essentially no difference between spontaneous and induced instability thresholds in the
case of metal pipes, this was thought to be related perhaps to the difference in material.
Indeed, there is a property of carbon-black-‘filled‘ rubbers known as ‘stress softening’,
but latex rubbers should be free of that. As shown in Chapter 5, the difference may be
related to the different ranges of L/Di involved subcritical Hopf bifurcation for relatively