Page 183 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

PIPES CONVEYING FLUID: LINEAR DYNAMICS I 165

Thus, the method of Section 3.3.6(a) may be used to solve the problem. As shown in
Section 2.1.4 and the discussion of Table 2.2, the method gives the correct results. In
the dimensionless version of the equation of motion, the location and magnitude of the
additional masses is expressed via

(3.124)

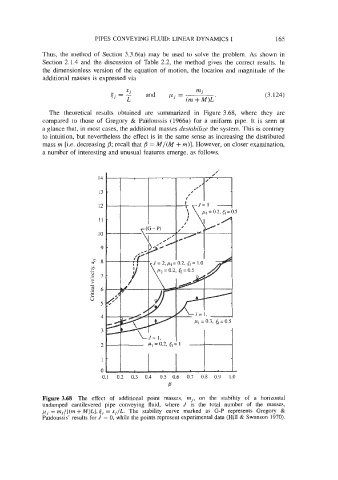
The theoretical results obtained are summarized in Figure 3.68, where they are
compared to those of Gregory & Paidoussis (1966a) for a uniform pipe. It is seen at
a glance that, in most cases, the additional masses destabilize the system. This is contrary
to intuition, but nevertheless the effect is in the same sense as increasing the distributed
mass m @e. decreasing B; recall that = M/(M + m)]. However, on closer examination,
a number of interesting and unusual features emerge, as follows.

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
P

Figure 3.68 The effect of additional point masses, mi, on the stability of a horizontal
undamped cantilevered pipe conveying fluid, where J is the total number of the masses,
wj = mj/[(m + M)L], ti = xj/L. The stability curve marked as G-P represents Gregory &
Pdidoussis’ results for J = 0, while the points represent experimental data (Hill & Swanson 1970).