Page 179 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

PIPES CONVEYING FLUID: LINEAR DYNAMICS I 161

there is some viscoelastic damping (even a = This demonstrates the difficulty
of the method in obtaining convergent results when the actual boundary conditions are
different from those of the comparison functions; the use of the delta function to incor-
porate the spring forces into the equation of motion is a useful artifice, but it does have
repercussions. However, with increasing dissipation (larger a), the higher mode content
is damped out, and this is why convergence is easier to achieve.
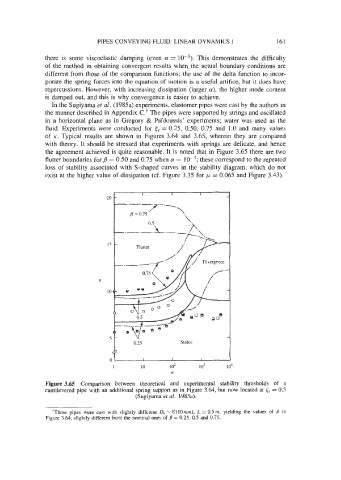
In the Sugiyama et al. (1985a) experiments, elastomer pipes were cast by the authors in
the manner described in Appendix C.+ The pipes were supported by strings and oscillated
in a horizontal plane as in Gregory & Paidoussis’ experiments; water was used as the
fluid. Experiments were conducted for tS = 0.25, 0.50, 0.75 and 1.0 and many values
of K. Typical results are shown in Figures 3.64 and 3.65, wherein they are compared
with theory. It should be stressed that experiments with springs are delicate, and hence
the agreement achieved is quite reasonable. It is noted that in Figure 3.65 there are two
flutter boundaries for ,8 = 0.50 and 0.75 when a = IO-’; these correspond to the repeated
loss of stability associated with S-shaped curves in the stability diagram, which do not
exist at the higher value of dissipation (cf. Figure 3.35 for /A = 0.065 and Figure 3.43).

15

U
10

V
Stable

1 10 IO2 1 o3 I o4
K
Figure 3.65 Comparison between theoretical and experimental stability thresholds of a
cantilevered pipe with an additional spring support as in Figure 3.64, but now located at = 0.5
(Sugiyama et at. 1985a).

+Three pipes were cast with slightly different Do - B(lOrnrn), L 2 0.5 rn, yielding the values of in
Figure 3.64, slightly different from the nominal ones of = 0.25, 0.5 and 0.75.