Page 176 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

158 SLENDER STRUCTURES AND AXIAL FLOW

now replaced by EZ(a3w/ax3) - Kw = 0, or in dimensionless form

a3 rl KL3
--q=O, K=-. (3.118)
at3 EI
Obviously, the method of solution of Section 3.3.6(a) may be utilized, except that the last
line of determinant (3.84) is now replaced by (a; - iK) exp(iaj), j = 1 - 4. Moreover,
working in a similar way as in Section 3.4.1, it is easy to find (Chen 1971a) that the
condition for divergence, u = ucd, is given by solutions of
3
u + K(sin u - u cos u) = 0. (3.1 19)

20

18

16

14

p = 0.6
p = 0.5
t

6

4 p=o+ Lp=o 1
I , I 111111~ , , ,,,,,,I , , , , I ,J
0.1 1 .o 10 100 loo0
K
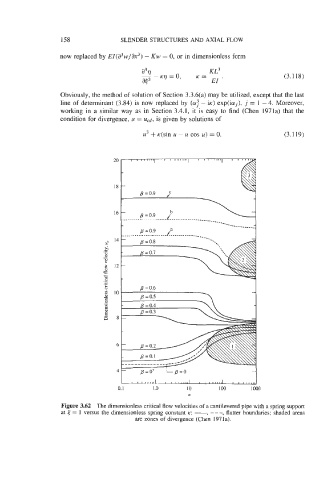
Figure 3.62 The dimensionless critical flow velocities of a cantilevered pipe with a spring support
at 6 = 1 versus the dimensionless spring constant K: -, - - - , flutter boundaries; shaded areas
are zones of divergence (Chen 1971a).