Page 174 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)
P. 174
156 SLENDER STRUCTURES AND AXIAL FLOW
by divergence, much as a clamped-pinned system would, but is also subject to flutter
at higher flow (generally single-mode flutter, not as the conservative system would).
Finally, for Z/L = Z,/L the two critical flow velocities become coincident and Chen &
Jendrzejczyk conjecture that this may lead to chaos (see Chapter 5).
The experiments were conducted with polyethylene pipes (0, 9.5 and 12.7 mm, wall
=
thickness h = 1.59mm, L = 685.8mm) with a ring-type knife edge support at varying
values of 1/L. The corresponding values of B were 0.48 and 0.60 approximately, while
y 2: 2 was sufficiently small for gravity effects to be neglected.
A great deal of high-quality data was obtained. Examples are shown in Figures 3.59
and 3.60. Some sample time traces for a pipe with Z/L = 0.25 (Zc/L E 0.35 in this case)
are shown in Figure 3.59(a) and display dynamical behaviour similar to that of a simple
cantilevered pipe as U is increased: (i) underdamped, (ii) and (iii) overdamped, (iv) again
underdamped, (v) limit-cycle oscillation and (vi) larger amplitude limit-cycle oscillation.
The oscillation in (i)-(v) was excited by perturbing the pipe, whereas in (vi) it developed
spontaneously. Measurements of the modal damping ratio on a nominally identical pipe
(but with B = 0.45) for varying Z/L, shown in Figure 3.59(b), document its precipitous
reduction as Ucf is approached.
1IL
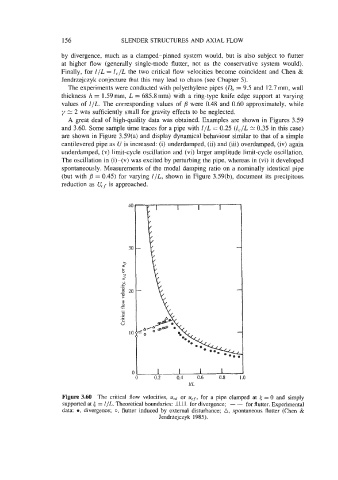
Figure 3.60 The critical flow velocities, uCd or ucf, for a pipe clamped at t = 0 and simply
supported at 6 = l/L. Theoretical boundaries: UV for divergence; - - for flutter. Experimental
data: 0, divergence; 0, flutter induced by external disturbance; A, spontaneous flutter (Chen &
Jendrzejczyk 1985).