Page 178 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

160 SLENDER STRUCTURES AND AXIAL FLOW

K destabilizes the system. This is the first of many unusual occurrences associated with
these S-shaped curves, as we shall see.
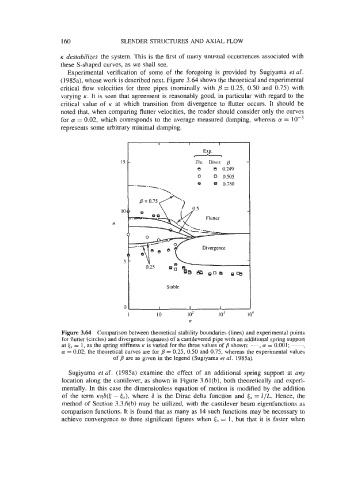
Experimental verification of some of the foregoing is provided by Sugiyama et al.
(1985a), whose work is described next. Figure 3.64 shows the theoretical and experimental
critical flow velocities for three pipes (nominally with ,9 = 0.25, 0.50 and 0.75) with
varying K. It is seen that agreement is reasonably good, in particular with regard to the
critical value of K at which transition from divergence to flutter occurs. It should be
noted that, when comparing flutter velocities, the reader should consider only the curves
for a = 0.02, which corresponds to the average measured damping, whereas a =
represents some arbitrary minimal damping.

Exp.
P A *
15 - Flu. Diver. /3 -
d 0 0.249
0 D 0.505
---. -. 0 13 0.780
\.

U

1 10 1 O2 1 o3 I o4
K
Figure 3.64 Comparison between theoretical stability boundaries (lines) and experimental points
for flutter (circles) and divergence (squares) of a cantilevered pipe with an additional spring support
at & = 1, as the spring stiffness K is varied for the three values of B shown: -.-, a! = 0.001; -,
a! = 0.02; the theoretical curves are for B = 0.25, 0.50 and 0.75, whereas the expenmental values
of B are as given in the legend (Sugiyama et al. 1985a).

Sugiyama et al. (1985a) examine the effect of an additional spring support at any
location along the cantilever, as shown in Figure 3.61(b), both theoretically and experi-
mentally. In this case the dimensionless equation of motion is modified by the addition
of the term ~$(t - e$), where 6 is the Dirac delta function and ts = Z/L. Hence, the
method of Section 3.3.6(b) may be utilized, with the cantilever beam eigenfunctions as
comparison functions. It is found that as many as 14 such functions may be necessary to
achieve convergence to three significant figures when .$ = 1, but that it is faster when