Page 196 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

178 SLENDER STRUCTURES AND AXIAL, FLOW

-1.0

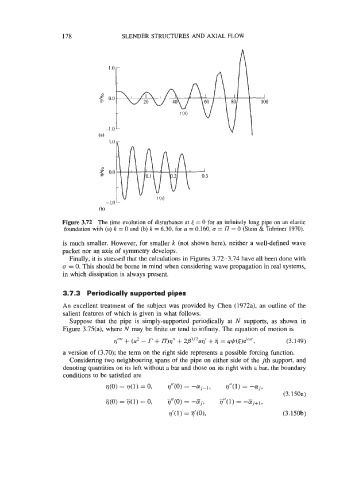
Figure 3.72 The time evolution of disturbance at 6 = 0 for an infinitely long pipe on an elastic
foundation with (a) k = 0 and (b) k = 6.30, for u = 0.160, CT = l7 = 0 (Stein & Tobriner 1970).
is much smaller. However, for smaller k (not shown here), neither a well-defined wave
packet nor an axis of symmetry develops.
Finally, it is stressed that the calculations in Figures 3.72-3.74 have all been done with
cr = 0. This should be borne in mind when considering wave propagation in real systems,
in which dissipation is always present.

3.7.3 Periodically supported pipes
An excellent treatment of the subject was provided by Chen (1972a), an outline of the
salient features of which is given in what follows.
Suppose that the pipe is simply-supported periodically at N supports, as shown in
Figure 3.75(a), where N may be finite or tend to infinity. The equation of motion is
+
Q”’’ + (u2 - r + WQ” 2p’/2ui7’ + ij = q+(6)eiur, (3.149)
a version of (3.70); the term on the right side represents a possible forcing function.
Considering two neighbouring spans of the pipe on either side of the jth support, and
denoting quantities on its left without a bar and those on its right with a bar, the boundary
conditions to be satisfied are

~(0) ~(1) = 0, ~”(0) -aj-1, ~”(1) = -aj,
=
=
(3.150a)
- -1’
Q(O> = ~(1) = 0, Q (0) = -Zj, $’(I) = -Zj+1,
Q’U) = 77’(0), (3.150b)