Page 198 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

180 SLENDER STRUCTURES AND AXIAL FLOW

1.0

0
E 0.0
c

-1.0
(a)

x = -100 ft

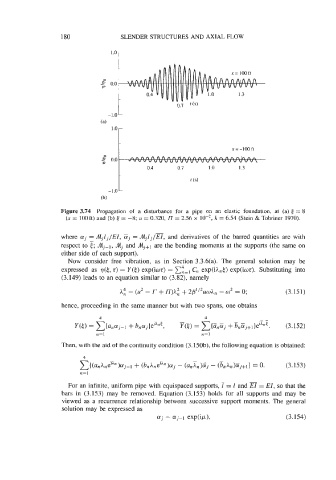
Figure 3.74 Propagation of a disturbance for a pipe on an elastic foundation, at (a) e = 8
(x = lOOft) and (b) 6 = -8; u = 0.320, Ij' = 2.56 x lo-', k = 6.54 (Stein & Tobriner 1970).

where aj 7 &,lj/EI, iij = Ajlj/a, and derivatives of the barred quantities are with
respect to 6; Aj-1, A, and .&,+I are the bending moments at the supports (the same on
either side of each support).
Now consider free vibration, as in Section 3.3.6(a). The general solution may be
expressed as 110, t) = Y(6) exp(iwt) = 4 C, exp(ihn6) exp(iot). Substituting into
(3.149) leads to an equation similar to (3.82), namely

- (u2 - r + np2, + 2,9'f2uwhn - w2 = 0; (3.151)

hence, proceeding in the same manner but with two spans, one obtains
4 - 4
Y(6) = C[anaj-l + bnaj]eih"', Y(6) = C[Zniij +bn5'!j+l}eii;nS. (3.152)
n=l n=l
Then, with the aid of the continuity condition (3.150b), the following equation is obtained:

4
C{(anineihn)aj-I + (bnhneiA")aj - (Z~X,,)~, - (bnZn)iij+I} 0. (3.153)
=
n=l
For an infinite, uniform pipe with equispaced supports, 1 = I and EI = EI, so that the
bars in (3.153) may be removed. Equation (3.153) holds for all supports and may be
viewed as a recurrence relationship between successive support moments. The general
solution may be expressed as
a, = aj-1 exp(ik), (3.154)