Page 278 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

PIPES CONVEYING FLUID: LINEAR DYNAMICS I1 259

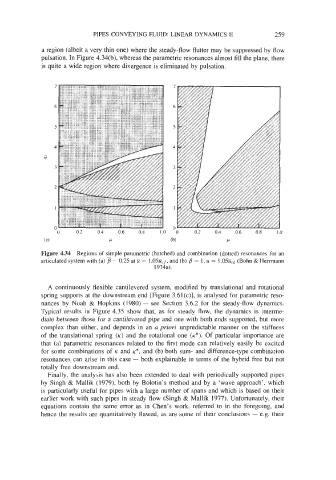
a region (albeit a very thin one) where the steady-flow flutter may be suppressed by flow
pulsation. In Figure 4.34(b), whereas the parametric resonances almost fill the plane, there
is quite a wide region where divergence is eliminated by pulsation.

0 0.2 0.4 0.6 0.8 1 .o ” 0 0.2 0.4 0.6 0.8 1.0
(a) P (b) P
Figure 4.34 Regions of simple parametric (hatched) and combination (dotted) resonances for an
articulated system with (a) 3 = 0.25 at U = 1.O5Ucf, and (b) B = 1, U = 1.05& (Bohn & Henmann
19744.

A continuously flexible cantilevered system, modified by translational and rotational
spring supports at the downstream end [Figure 3.61(c)], is analysed for parametric reso-
nances by Noah & Hopkins (1980) - see Section 3.6.2 for the steady-flow dynamics.
Typical results in Figure 4.35 show that, as for steady flow, the dynamics is interme-
diate between those for a cantilevered pipe and one with both ends supported, but more
complex than either, and depends in an a priori unpredictable manner on the stiffness
of the translational spring (K) and the rotational one (K*). Of particular importance are
that (a) parametric resonances related to the first mode can relatively easily be excited
for some combinations of K and K*, and (b) both sum- and difference-type combination
resonances can arise in this case - both explainable in terms of the hybrid free but not
totally free downstream end.
Finally, the analysis has also been extended to deal with periodically supported pipes
by Singh & Mallik (1979), both by Bolotin’s method and by a ‘wave approach’, which
is particularly useful for pipes with a large number of spans and which is based on their
earlier work with such pipes in steady flow (Singh & Mallik 1977). Unfortunately, their
equations contain the same error as in Chen’s work, referred to in the foregoing, and
hence the results are quantitatively flawed, as are some of their conclusions - e.g. their