Page 275 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)
P. 275
256 SLENDER STRUCTURES AND AXIAL FLOW
encountered, which were no different in character from those associated with the second
mode. However, no simple parametric (as opposed to combination) resonances associated
with the first mode were ever observed.
In one case, the flow velocity was increased sufficiently to cause flutter in steady flow.
Interestingly, by adding a pulsatile component to the flow at certain frequencies and
amplitudes, it was found possible to eliminate the flutter.
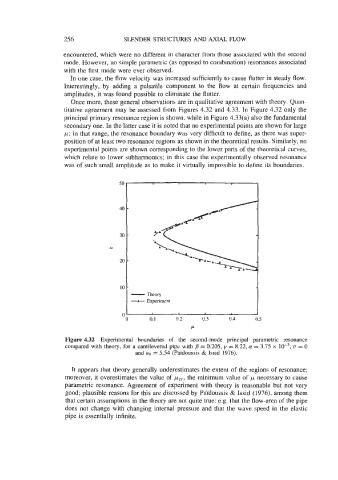
Once more, these general observations are in qualitative agreement with theory. Quan-
titative agreement may be assessed from Figures 4.32 and 4.33. In Figure 4.32 only the
principal primary resonance region is shown, while in Figure 4.33(a) also the fundamental
secondary one. In the latter case it is noted that no experimental points are shown for large
k; in that range, the resonance boundary was very difficult to define, as there was super-
position of at least two resonance regions as shown in the theoretical results. Similarly, no
experimental points are shown corresponding to the lower parts of the theoretical curves,
which relate to lower subharmonics; in this case the experimentally observed resonance
was of such small amplitude as to make it virtually impossible to define its boundaries.
40 .
30 .
0
20 '
10 '
- Theory
-A- Experiment
0
0 0.1 0.2 0.3 0.4 0.5
@
Figure 4.32 Experimental boundaries of the second-mode principal parametric resonance
compared with theory, for a cantilevered pipe with /? = 0.205, y = 8.22, a! = 3.75 x 0 = 0
and uo = 5.54 (Paidoussis & Issid 1976).
It appears that theory generally underestimates the extent of the regions of resonance;
moreover, it overestimates the value of wcr, the minimum value of k necessary to cause
parametric resonance. Agreement of experiment with theory is reasonable but not very
good; plausible reasons for this are discussed by Pdidoussis & Issid (1976), among them
that certain assumptions in the theory are not quite true: e.g. that the flow-area of the pipe
does not change with changing internal pressure and that the wave speed in the elastic
pipe is essentially infinite.