Page 276 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)
P. 276
PIPES CONVEYING FLUID: LINEAR DYNAMICS I1 257
,:: ::::::-......
20 I
6J 10 -
0 I
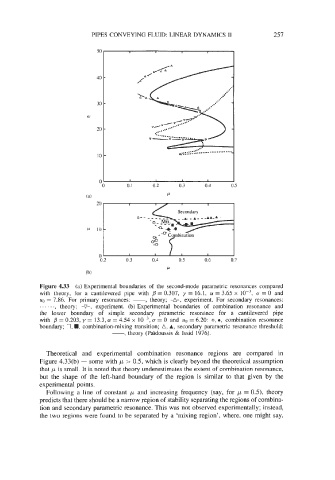
Figure 4.33 (a) Experimental boundaries of the second-mode parametric resonances compared
with theory, for a cantilevered pipe with /3 = 0.307, y = 16.1, CY = 3.65 x u = 0 and
uo = 7.86. For primary resonances: -, theory; -A-, experiment. For secondary resonances:
f..... , theory; -v-, experiment. (b) Experimental boundaries of combination resonance and
the lower boundary of simple secondary parametric resonance for a cantilevered pipe
with /3 = 0.203, y = 13.3, (Y = 4.54 x (J = 0 and uo = 6.20: 0, 0, combination resonance
boundary; 0, W, combination-mixing transition; A, A, secondary parametric resonance threshold;
-, theory (Pafdoussis & Issid 1976).
Theoretical and experimental combination resonance regions are compared in
Figure 4.33(b) - some with p =- 0.5, which is clearly beyond the theoretical assumption
that p is small. It is noted that theory underestimates the extent of combination resonance,
but the shape of the left-hand boundary of the region is similar to that given by the
experimental points.
Following a line of constant p and increasing frequency (say, for p = OS), theory
predicts that there should be a narrow region of stability separating the regions of combina-
tion and secondary parametric resonance. This was not observed experimentally; instead,
the two regions were found to be separated by a 'mixing region', where, one might say,