Page 274 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)
P. 274
PIPES CONVEYING FLUID: LINEAR DYNAMICS I1 255
40
30
w
A .
20 , , \ A ‘
. . . . . . .
-V-
I... *...
I
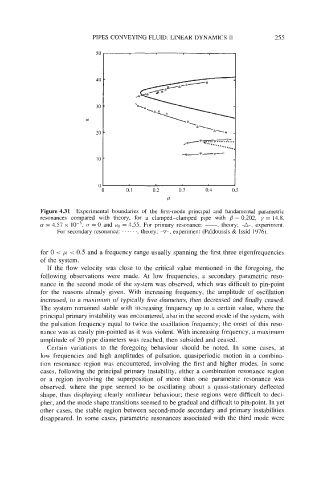
Figure 4.31 Experimental boundaries of the first-mode principal and fundamental parametric
resonances compared with theory, for a clamped-clamped pipe with B = 0.202, y = 14.8,
cr = 4.57 x (T = 0 and uo = 4.55. For primary resonance: -, theory; -A-, experiment.
For secondary resonance: . . . . . ., theory; -v-, experiment (Pai‘doussis & Issid 1976).
for 0 < p < 0.5 and a frequency range usually spanning the first three eigenfrequencies
of the system.
If the flow velocity was close to the critical value mentioned in the foregoing, the
following observations were made. At low frequencies, a secondary parametric reso-
nance in the second mode of the system was observed, which was difficult to pin-point
for the reasons already given. With increasing frequency, the amplitude of oscillation
increased, to a maximum of typically five diameters, then decreased and finally ceased.
The system remained stable with increasing frequency up to a certain value, where the
principal primary instability was encountered, also in the second mode of the system, with
the pulsation frequency equal to twice the oscillation frequency; the onset of this reso-
nance was as easily pin-pointed as it was violent. With increasing frequency, a maximum
amplitude of 20 pipe diameters was reached, then subsided and ceased.
Certain variations to the foregoing behaviour should be noted. In some cases, at
low frequencies and high amplitudes of pulsation, quasiperiodic motion in a combina-
tion resonance region was encountered, involving the first and higher modes. In some
cases, following the principal primary instability, either a combination resonance region
or a region involving the superposition of more than one parametric resonance was
observed, where the pipe seemed to be oscillating about a quasi-stationary deflected
shape, thus displaying clearly nonlinear behaviour; these regions were difficult to deci-
pher, and the mode shape transitions seemed to be gradual and difficult to pin-point. In yet
other cases, the stable region between second-mode secondary and primary instabilities
disappeared. In some cases, parametric resonances associated with the third mode were