Page 270 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

PIPES CONVEYING FLUID: LINEAR DYNAMICS II 25 1

7

6

w
5 2 2
WOI

4

Is"
w1+ 02
wo1
3

2

1

n
0 0.1 0.2 0.3 0.4 0.5
P

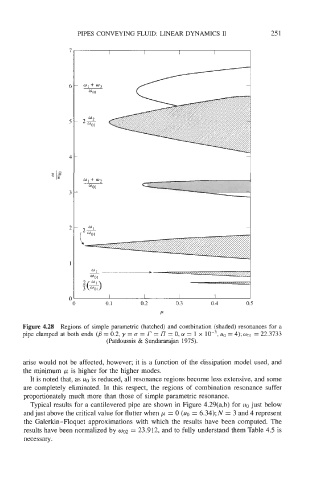
Figure 4.28 Regions of simple parametric (hatched) and combination (shaded) resonances for a
pipe clamped at both ends (j3 = 0.2, y = c = r = l7 = 0, a = 1 x uo = 4); 001 = 22.3733
(Pdidoussis & Sundararajan 1975).

arise would not be affected, however; it is a function of the dissipation model used, and
the minimum p is higher for the higher modes.
It is noted that, as uo is reduced, all resonance regions become less extensive, and some
are completely eliminated. In this respect, the regions of combination resonance suffer
proportionately much more than those of simple parametric resonance.
Typical results for a cantilevered pipe are shown in Figure 4.29(a,b) for uo just below
and just above the critical value for flutter when p = 0 (UO = 6.34); N = 3 and 4 represent
the Galerkin-Floquet approximations with which the results have been computed. The
results have been normalized by w02 = 23.912, and to fully understand them Table 4.5 is
necessary.