Page 268 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

PIPES CONVEYING FLUID: LINEAR DYNAMICS I1 249
-
- I I I I -
2.8
-
2.6
-
2.4
-
2.2
-
2.0
-
1.8
-
1.6
-
1.4
1.2 -
-
1.0
-
0.8
-
0.6
". . 0.4 I I I I I
0 0.1 0.2 0.3 0.4 0.5 0 0.1 0.2 0.3 0.4 0.5
Y

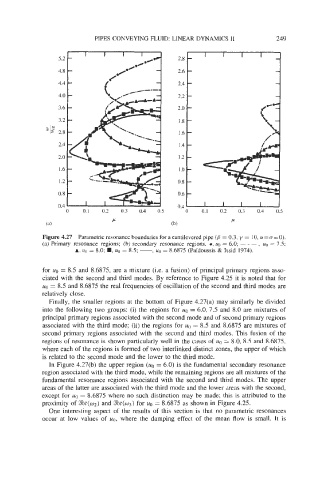
Figure 4.27 Parametric resonance boundaries for a cantilevered pipe (p = 0.3, y = 10, a = G = 0).
(a) Primary resonance regions; (b) secondary resonance regions. 0, uo = 6.0; - - , z40 = 7.5;
-
A, UO = 8.0; ., 8.5; -, uo = 8.6875 (Pai'doussis & Issid 1974).
=
uo
for uo = 8.5 and 8.6875, are a mixture (i.e. a fusion) of principal primary regions asso-
ciated with the second and third modes. By reference to Figure 4.25 it is noted that for
uo = 8.5 and 8.6875 the real frequencies of oscillation of the second and third modes are
relatively close.
Finally, the smaller regions at the bottom of Figure 4.27(a) may similarly be divided
into the following two groups: (i) the regions for uo = 6.0,7.5 and 8.0 are mixtures of
principal primary regions associated with the second mode and of second primary regions
associated with the third mode; (ii) the regions for uo = 8.5 and 8.6875 are mixtures of
second primary regions associated with the second and third modes. This fusion of the
regions of resonance is shown particularly well in the cases of uo = 8.0, 8.5 and 8.6875.
where each of the regions is formed of two interlinked distinct zones, the upper of which
is related to the second mode and the lower to the third mode.
In Figure 4.27(b) the upper region (UO = 6.0) is the fundamental secondary resonance
region associated with the third mode, while the remaining regions are all mixtures of the
fundamental resonance regions associated with the second and third modes. The upper
areas of the latter are associated with the third mode and the lower a-eas with the second,
except for uo = 8.6875 where no such distinction may be made; this is attributed to the
proximity of %e(W2) and %e(03) for uo = 8.6875 as shown in Figure 4.25.
One interesting aspect of the results of this section is that no parametric resonances
occur at low values of Ug, where the damping effect of the mean flow is small. It is