Page 265 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

246 SLENDER STRUCTURES AND AXIAL FLOW

I I I I
2.0

1.8

1.0 : uo= 1 -

uo = 1.8
0.8 ' 1 I 1 1 I

0 0.1 0.2 0.3 0.4 0.5
P

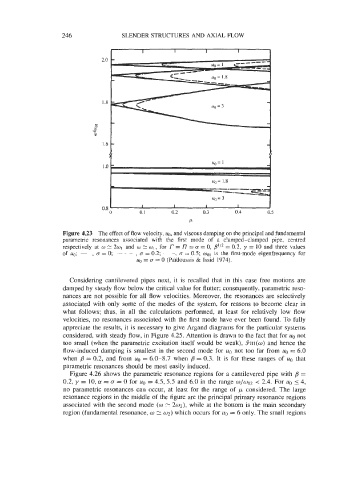
Figure 4.23 The effect of flow velocity, UO, and viscous damping on the principal and fundamental
parametric resonances associated with the first mode of a clamped-clamped pipe, centred
respectively at w E 2wl and w 2: w1, for f = I7 = (Y = 0, = 0.2, y = 10 and three values
of uo; -, CJ = 0; - - , CJ = 0.2; ---, CJ = 0.5; wol is the first-mode eigenfrequency for
-
uo = (T = 0 (Pai'doussis & Issid 1974).

Considering cantilevered pipes next, it is recalled that in this case free motions are
damped by steady flow below the critical value for flutter; consequently, parametric reso-
nances are not possible for all flow velocities. Moreover, the resonances are selectively
associated with only some of the modes of the system, for reasons to become clear in
what follows; thus, in all the calculations performed, at least for relatively low flow
velocities, no resonances associated with the first mode have ever been found. To fully
appreciate the results, it is necessary to give Argand diagrams for the particular systems
considered, with steady flow, in Figure 4.25. Attention is drawn to the fact that for uo not
too small (when the parametric excitation itself would be weak), 9m(w) and hence the
flow-induced damping is smallest in the second mode for uo not too far from uo = 6.0
when /3 = 0.2, and from uo = 6.0-8.7 when /3 = 0.3. It is for these ranges of uo that
parametric resonances should be most easily induced.
Figure 4.26 shows the parametric resonance regions for a cantilevered pipe with p =
0.2, y = 10, a = (T = 0 for uo = 4.5,5.5 and 6.0 in the range w/wo2 c 2.4. For uo 5 4,
no parametric resonances can occur, at least for the range of j~ considered. The large
resonance regions in the middle of the figure are the principal primary resonance regions
associated with the second mode (w 2 2w2), while at the bottom is the main secondary
region (fundamental resonance, w 2: w2) which occurs for uo = 6 only. The small regions