Page 267 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

248 SLENDER STRUCTURES AND AXIAL FLOW

L

I 1 1 I I
0 0.1 0.2 0.3 0.4 0.5
P
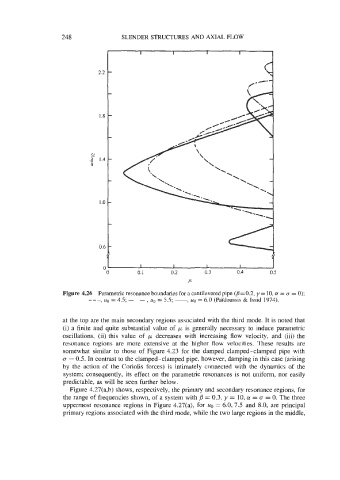
Figure 4.26 Parametric resonance boundaries for a cantilevered pipe (8=0.2, y = 10, a = CT = 0);
--_ , u0 = 4.5; - - , uo = 5.5; -, uo = 6.0 (PaYdoussis & Issid 1974).
-

at the top are the main secondary regions associated with the third mode. It is noted that
(i) a finite and quite substantial value of p is generally necessary to induce parametric
oscillations, (ii) this value of p decreases with increasing flow velocity, and (iii) the
resonance regions are more extensive at the higher flow velocities. These results are
somewhat similar to those of Figure 4.23 for the damped clamped-clamped pipe with
CT = 0.5. In contrast to the clamped-clamped pipe, however, damping in this case (arising
by the action of the Coriolis forces) is intimately connected with the dynamics of the
system; consequently, its effect on the parametric resonances is not uniform, nor easily
predictable, as will be seen further below.
Figure 4.27(a,b) shows, respectively, the primary and secondary resonance regions, for
the range of frequencies shown, of a system with B = 0.3, y = 10, a = CT = 0. The three
uppermost resonance regions in Figure 4.27(a), for uo = 6.0, 7.5 and 8.0, are principal
primary regions associated with the third mode, while the two large regions in the middle,