Page 362 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

342 SLENDER STRUCTURES AND AXIAL FLOW

-56 -54 -52 -50 43 46 44 42 40 -38
Gravity parameter, y
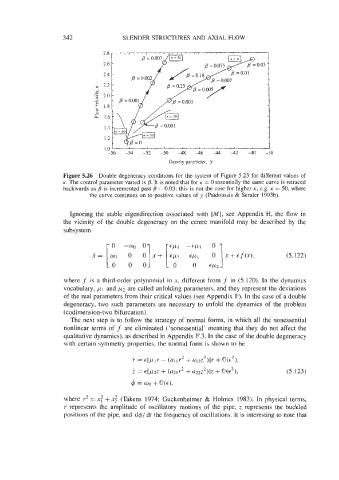
Figure 5.26 Double degeneracy conditions for the system of Figure 5.23 for different values of
K. The control parameter varied is B. It is noted that for K = 0 essentially the same curve is retraced
backwards as #3 is incremented past = 0.03; this is not the case for higher K, e.g. K = 50. where
the curve continues on to positive values of y (Pai’doussis & Semler 1993b).

Ignoring the stable eigendirection associated with [MI, see Appendix H, the flow in
the vicinity of the double degeneracy on the centre manifold may be described by the
subsystem

where f is a third-order polynomial in x, different from f in (5.120). In the dynamics
vocabulary, pi and ,u2 are called unfolding parameters, and they represent the deviations
of the real parameters from their critical values (see Appendix F). In the case of a double
degeneracy, two such parameters are necessary to unfold the dynamics of the problem
(codimension-two bifurcation).
The next step is to follow the strategy of normal forms, in which all the nonessential
nonlinear terms of f are eliminated (‘nonessential’ meaning that they do not affect the
qualitative dynamics), as described in Appendix F.3. In the case of the double degeneracy
with certain symmetry properties, the normal form is shown to be

where r2 = x: + x; (Takens 1974; Guckenheimer & Holmes 1983). In physical terms,
Y represents the amplitude of oscillatory motions of the pipe, z represents the buckled
positions of the pipe, and d4/ dt the frequency of oscillations. It is interesting to note that