Page 359 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

PIPES CONVEYING FLUID: NONLINEAR AND CHAOTIC DYNAMICS 339

I I I '\
I u= 15.07
I
I
I

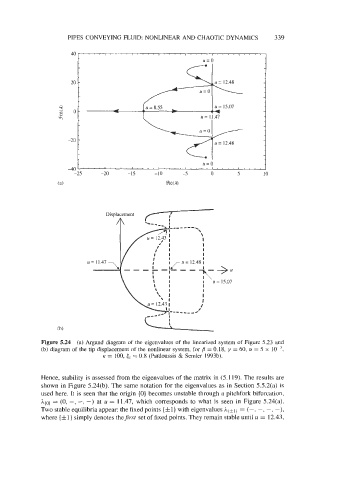
Figure 5.24 (a) Argand diagram of the eigenvalues of the linearized system of Figure 5.23 and
(b) diagram of the tip displacement of the nonlinear system, for j3 = 0.18, y = 60, (Y = 5 x
K = 100, & = 0.8 (Pa'idoussis & Semler 1993b).

Hence, stability is assessed from the eigenvalues of the matrix in (5.1 19). The results are
shown in Figure 5.24(b). The same notation for the eigenvalues as in Section 5.5.2(a) is
used here. It is seen that the origin (0) becomes unstable through a pitchfork bifurcation,
h{o~ = (0, -, -, -) at u = 11.47, which corresponds to what is seen in Figure 5.24(a).
Two stable equilibria appear: the fixed points (fl} with eigenvalues A,*l) = (-, -, -, -),
where {kl} simply denotes theJirst set of fixed points. They remain stable until u = 12.43,