Page 354 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

334 SLENDER STRUCTURES AND AXIAL FLOW

I I I I
--- Planar supercritical
Circular supercritical

0.873
A

I

0 0.2 0.4 0.6 0.8 0.9
B
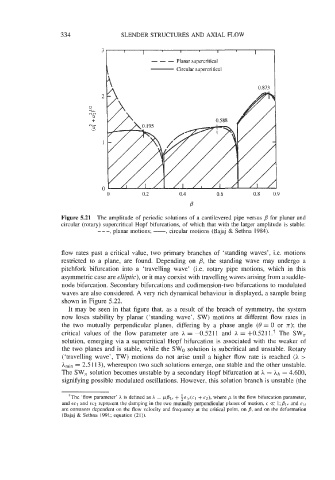
Figure 5.21 The amplitude of periodic solutions of a cantilevered pipe versus j3 for planar and
circular (rotary) supercritical Hopf bifurcations, of which that with the larger amplitude is stable:
___ , planar motions; -, circular motions (Bajaj & Sethna 1984).

flow rates past a critical value, two primary branches of ‘standing waves’, i.e. motions
restricted to a plane, are found. Depending on B, the standing wave may undergo a
pitchfork bifurcation into a ‘travelling wave’ (Le. rotary pipe motions, which in this
asymmetric case are elliptic), or it may coexist with travelling waves arising from a saddle-
node bifurcation. Secondary bifurcations and codimension-two bifurcations to modulated
waves are also considered. A very rich dynamical behaviour is displayed, a sample being
shown in Figure 5.22.
It may be seen in that figure that, as a result of the breach of symmetry, the system
now loses stability by planar (‘standing wave’, SW) motions at different flow rates in
the two mutually perpendicular planes, differing by a phase angle (0 = 0 or n); the
critical values of the flow parameter are h = -0.5211 and h = +0.5211.+ The SW,
solution, emerging via a supercritical Hopf bifurcation is associated with the weaker of
the two planes and is stable, while the SWO solution is subcritical and unstable. Rotary
(‘travelling wave’, TW) motions do not arise until a higher flow rate is reached (h >
Amin = 2.5113), whereupon two such solutions emerge, one stable and the other unstable.
The SW, solution becomes unstable by a secondary Hopf bifurcation at h = hh = 4.600,
signifying possible modulated oscillations. However, this solution branch is unstable (the

+The ‘flow parameter’ A is defined as A = pplr + ieli(cl + CZ), where is the flow bifurcation parameter,
and ECI and ECZ represent the damping in the two mutually perpendicular planes of motion. c << 1;j31r and eli
are constants dependent on the flow velocity and frequency at the critical point, on B. and on the deformation
(Bajaj & Sethna 1991; equation (21)).