Page 350 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

330 SLENDER STRUCTURES AND AXIAL FLOW

15

10

5
xu
9
0

-5

-10

-15
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
(b) P
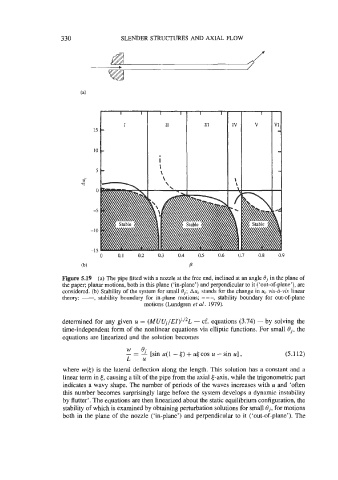
Figure 5.19 (a) The pipe fitted with a nozzle at the free end, inclined at an angle 0, in the plane of
the paper; planar motions, both in this plane (‘in-plane’) and perpendicular to it (‘out-of-plane’), are
considered. (b) Stability of the system for small 0,; AuC stands for the change in uc vis-a-vis linear
theory: -, stability boundary for in-plane motions; - - -, stability boundary for out-of-plane
motions (Lundgren et aE. 1979).

determined for any given u = (MUt.Jj/EI)1/2L - cf. equations (3.74) - by solving the
time-independent form of the nonlinear equations via elliptic functions. For small e,, the
equations are linearized and the solution becomes

(5.112)

where w(() is the lateral deflection along the length. This solution has a constant and a
linear term in 4, causing a tilt of the pipe from the axial (-axis, while the trigonometric part
indicates a wavy shape. The number of periods of the waves increases with u and ‘often
this number becomes surprisingly large before the system develops a dynamic instability
by flutter’. The equations are then linearized about the static equilibrium configuration, the
stability of which is examined by obtaining perturbation solutions for small e,, for motions
both in the plane of the nozzle (‘in-plane’) and perpendicular to it (‘out-of-plane’). The