Page 347 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

PIPES CONVEYING FLUID: NONLINEAR AND CHAOTIC DYNAMICS 327

0.05

-0.1 -0.05 0 0.05 0.1

r2 I 0.1 I I I I I

0.05

$1 0

-0.05

-0.1
rl -0.15 -0.1 -0.05 0 0.05 0.1 0.15

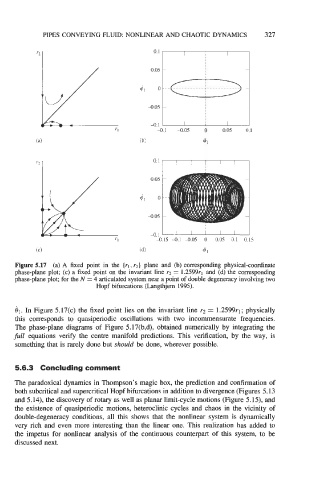
Figure 5.17 (a) A fixed point in the [rl, rz] plane and (b) corresponding physical-coordinate
phase-plane plot; (c) a fixed point on the invariant line r2 = 1.2599r1 and (d) the corresponding
phase-plane plot; for the N = 4 articulated system near a point of double degeneracy involving two
Hopf bifurcations (Langthjem 1995).

&. In Figure 5.17(c) the fixed point lies on the invariant line r2 = 1.2599r-l; physically
this corresponds to quasiperiodic oscillations with two incommensurate frequencies.
The phase-plane diagrams of Figure 5.17(b,d), obtained numerically by integrating the
full equations verify the centre manifold predictions. This verification, by the way, is
something that is rarely done but should be done, wherever possible.

5.6.3 Concluding comment
The paradoxical dynamics in Thompson’s magic box, the prediction and confirmation of
both subcritical and supercritical Hopf bifurcations in addition to divergence (Figures 5.13
and 5.14), the discovery of rotary as well as planar limit-cycle motions (Figure 5.19, and
the existence of quasiperiodic motions, heteroclinic cycles and chaos in the vicinity of
double-degeneracy conditions, all this shows that the nonlinear system is dynamically
very rich and even more interesting than the linear one. This realization has added to
the impetus for nonlinear analysis of the continuous counterpart of this system, to be
discussed next.