Page 349 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

PIPES CONVEYING FLUID: NONLINEAR AND CHAOTIC DYNAMICS 329

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
B

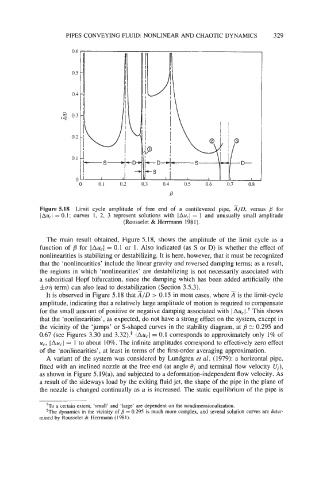
Figure 5.18 Limit cycle amplitude of free end of a cantilevered pipe, AID, versus B for
IAu,l = 0.1; curves 1, 2, 3 represent solutions with IAu,l = 1 and unusually small amplitude
(Rousselet & Herrmann 1981).

The main result obtained, Figure 5.18, shows the amplitude of the limit cycle as a
function of B for lAu,l = 0.1 or 1. Also indicated (as S or D) is whether the effect of
nonlinearities is stabilizing or destabilizing. It is here, however, that it must be recognized
that the ‘nonlinearities’ include the linear gravity and reversed damping terms; as a result,
the regions in which ‘nonlinearities’ are destabilizing is not necessarily associated with
a subcritical Hopf bifurcation, since the damping which has been added artificially (the
ktarj term) can also lead to destabilization (Section 3.5.3).
It is observed in Figure 5.18 that AID > 0.15 in most cases, where A is the limit-cycle
amplitude, indicating that a relatively large amplitude of motion is required to compensate
for the small amount of positive or negative damping associated with IAu,~.~ This shows
that the ‘nonlinearities’, as expected, do not have a strong effect on the system, except in
the vicinity of the ‘jumps’ or S-shaped curves in the stability diagram, at B E 0.295 and
0.67 (see Figures 3.30 and 3.32).* IAu,l = 0.1 corresponds to approximately only 1% of
u,, IAu,l = 1 to about 10%. The infinite amplitudes correspond to effectively zero effect
of the ‘nonlinearities’, at least in terms of the first-order averaging approximation.
A variant of the system was considered by Lundgren et al. (1979): a horizontal pipe,
fitted with an inclined nozzle at the free end (at angle 0, and terminal flow velocity Uj),
as shown in Figure 5.19(a), and subjected to a deformation-independent flow velocity. As
a result of the sideways load by the exiting fluid jet, the shape of the pipe in the plane of
the nozzle is changed continually as u is increased. The static equilibrium of the pipe is

+To a certain extent, ‘small’ and ‘large’ are dependent on the nondimensionalization.
$The dynamics in the vicinity of @ = 0.295 is much more complex, and several solution curves are deter-
mined by Rousselet & Henmann (1981).