Page 352 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

332 SLENDER STRUCTURES AND AXIAL FLOW

‘.O t Supercritical

0.8

(Y 0.6

0.4

0.2

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
P

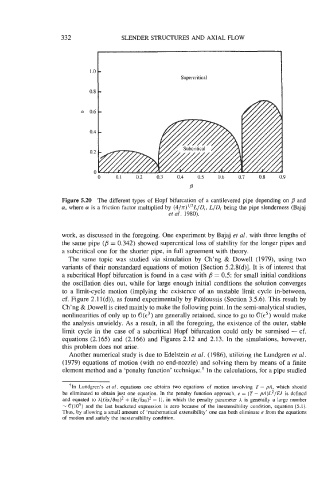
Figure 5.20 The different types of Hopf bifurcation of a cantilevered pipe depending on #? and
a, where a is a friction factor multiplied by (4/rr)’/*L/Di, LIDi being the pipe slenderness (Bajaj
et al. 1980).

work, as discussed in the foregoing. One experiment by Bajaj et al. with three lengths of
the same pipe (B = 0.342) showed supercritical loss of stability for the longer pipes and
a subcritical one for the shorter pipe, in full agreement with theory.
The same topic was studied via simulation by Ch’ng & Dowell (1979), using two
variants of their nonstandard equations of motion [Section 5.2.8(d)]. It is of interest that
a subcritical Hopf bifurcation is found in a case with B = 0.5: for small initial conditions
the oscillation dies out, while for large enough initial conditions the solution converges
to a limit-cycle motion (implying the existence of an unstable limit cycle in-between,
cf. Figure 2.11(d)), as found experimentally by Pdidoussis (Section 3.5.6). This result by
Ch’ng & Dowell is cited mainly to make the following point. In the semi-analytical studies,
nonlinearities of only up to 0(c3) are generally retained, since to go to 0(c5) would make
the analysis unwieldy. As a result, in all the foregoing, the existence of the outer, stable
limit cycle in the case of a subcritical Hopf bifurcation could only be surmised - cf.
equations (2.165) and (2.166) and Figures 2.12 and 2.13. In the simulations, however,
this problem does not arise.
Another numerical study is due to Edelstein et al. (1986), utilizing the Lundgren et al.
(1979) equations of motion (with no end-nozzle) and solving them by means of a finite
element method and a ‘penalty function’ technique.+ In the calculations, for a pipe studied

+In Lundgren’s et al. equations one obtains two equations of motion involving T - PA, which should
be eliminated to obtain just one equation. In the penalty function approach, e = (T - pA)L2/EZ is defined
and equated to h.[(ax/ax~)~ + (&/&GO)~ - I], in which the penalty parameter h is generally a large number
- 0(105) and the last bracketed expression is zero because of the inextensibility condition, equation (5.1).
Thus, by allowing a small amount of ‘mathematical extensibility’ one can both eliminate e from the equations
of motion and satisfy the inextensibility condition.