Page 411 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

386 SLENDER STRUCTURES AND AXIAL FLOW

0.02

-0.02
h
+
+
v
P(
4.04 O’Ol

-0.06

-0.08
-0.08 -0.06 4.04 -0.02 0.0 0.02
(b) 4 ,(n)
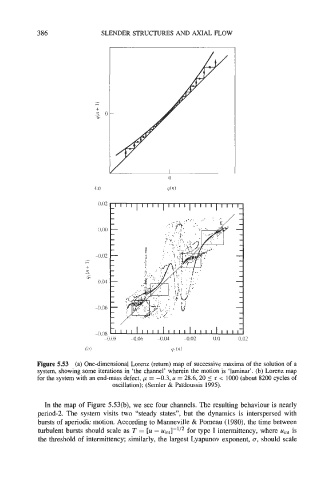
Figure 5.53 (a) One-dimensional Lorenz (return) map of successive maxima of the solution of a
system, showing some iterations in ‘the channel’ wherein the motion is ‘laminar’. (b) Lorenz map
for the system with an end-mass defect, p = -0.3, u = 28.6,20 5 t i lo00 (about 8200 cycles of
oscillation); (Semler & Pdidoussis 1995).

In the map of Figure 5.53(b), we see four channels. The resulting behaviour is nearly
period-2. The system visits two “steady states”, but the dynamics is interspersed with
bursts of aperiodic motion. According to Manneville & Pomeau (1980), the time between
turbulent bursts should scale as T = [u - uint]-”* for type I intermittency, where Uint is
the threshold of intermittency; similarly, the largest Lyapunov exponent, 0, should scale