Page 485 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

CURVED PIPES CONVEYING FLUID 455

4 I I I I I I I I I i

3 \
+ 3.5 - Values of ii*
I \
I \, ,4th mode
0 2.5 \
I \ \
I
2 I ‘93
P2 \ \ \
*
h
3 I \ ‘p2.5
v I \
.. - A h \
c
4 I h2
I- 1st mode ‘P2 3rd mode
\,,
‘,
- I 4 \
I 9
\
A
2
v
0
\
\
44

-1
0 2 4 6 8 10
%e (O*)
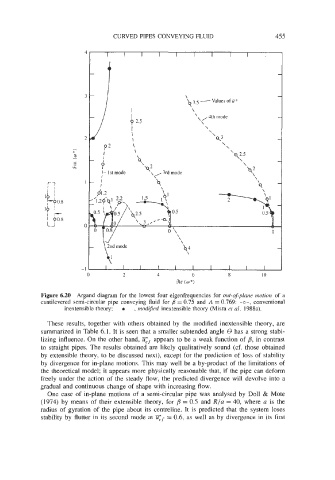
Figure 6.20 Argand diagram for the lowest four eigenfrequencies for out-of-plane motion of a
cantilevered semi-circular pipe conveying fluid for = 0.75 and A = 0.769: -0-, conventional
inextensible theory; - - 0 - , modified inextensible theory (Misra et al. 1988a).

These results, together with others obtained by the modified inextensible theory, are
summarized in Table 6.1. It is seen that a smaller subtended angle 0 has a strong stabi-
lizing influence. On the other hand, ETf appears to be a weak function of p, in contrast
to straight pipes. The results obtained are likely qualitatively sound (cf. those obtained
by extensible theory, to be discussed next), except for the prediction of loss of stability
by divergence for in-plane motions. This may well be a by-product of the limitations of
the theoretical model; it appears more physically reasonable that, if the pipe can deform
freely under the action of the steady flow, the predicted divergence will devolve into a
gradual and continuous change of shape with increasing flow.
One case of in-plane motions of a semi-circular pipe was analysed by Doll & Mote
(1974) by means of their extensible theory, for p = 0.5 and R/a = 40, where a is the
radius of gyration of the pipe about its centreline. It is predicted that the system loses
stability by flutter in its second mode at UTf = 0.6, as well as by divergence in its first