Page 487 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

CURVED PIPES CONVEYING FLUID 457

,

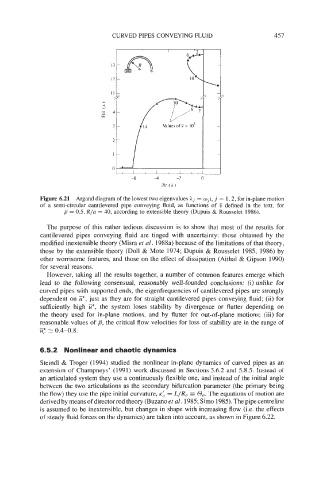
Figure 6.21 Argand diagram of the lowest two eigenvalues hj = wji, j = 1, 2, for in-plane motion
of a semi-circular cantilevered pipe conveying fluid, as functions of V defined in the text, for
= 0.5, R/a = 40, according to extensible theory (Dupuis & Rousselet 1986).

The purpose of this rather tedious discussion is to show that most of the results for
cantilevered pipes conveying fluid are tinged with uncertainty: those obtained by the
modified inextensible theory (Misra et al. 1988a) because of the limitations of that theory,
those by the extensible theory (Doll & Mote 1974; Dupuis & Rousselet 1985, 1986) by
other worrisome features, and those on the effect of dissipation (Aithal & Gipson 1990)
for several reasons.
However, taking all the results together, a number of common features emerge which
lead to the following consensual, reasonably well-founded conclusions: (i) unlike for
curved pipes with supported ends, the eigenfrequencies of cantilevered pipes are strongly
dependent on E*, just as they are for straight cantilevered pipes conveying fluid; (ii) for
sufficiently high E*, the system loses stability by divergence or flutter depending on
the theory used for in-plane motions, and by flutter for out-of-plane motions; (iii) for
reasonable values of /?, the critical flow velocities for loss of stability are in the range of
-
UF 2: 0.4-0.8.

6.5.2 Nonlinear and chaotic dynamics

Steindl & Troger (1994) studied the nonlinear in-plane dynamics of curved pipes as an
extension of Champneys’ (1991) work discussed in Sections 5.6.2 and 5.8.5. Instead of
an articulated system they use a continuously flexible one, and instead of the initial angle
between the two articulations as the secondary bifurcation parameter (the primary being
the flow) they use the pipe initial curvature, K: = L/Ro = 0,. The equations of motion are
derived by means of director rod theory (Buzano et al. 1985; Simo 1985). The pipe centreline
is assumed to be inextensible, but changes in shape with increasing flow (i.e. the effects
of steady fluid forces on the dynamics) are taken into account, as shown in Figure 6.22.