Page 491 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

CURVED PIPES CONVEYING FLUID 46 1
m

0 20 40 60 80
%ne (w*)
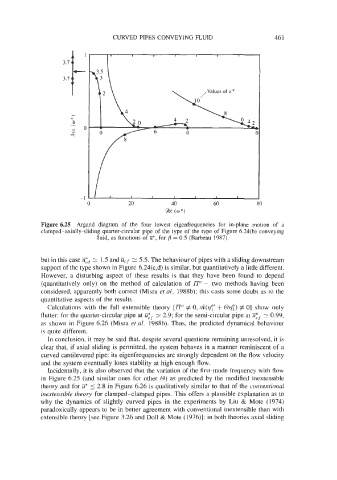
Figure 6.25 Argand diagram of the four lowest eigenfrequencies for in-plane motion of a
clamped-axially-sliding quarter-circular pipe of the type of the type of Figure 6.24(b) conveying
fluid, as functions of E*, for /3 = 0.5 (Barbeau 1987).

but in this case ii:d 2 1.5 and iicf 2 5.5. The behaviour of pipes with a sliding downstream
support of the type shown in Figure 6.24(c,d) is similar, but quantitatively a little different.
However, a disturbing aspect of these results is that they have been found to depend
(quantitatively only) on the method of calculation of l7* - two methods having been
considered, apparently both correct (Misra et al. 1988b); this casts some doubt as to the
quantitative aspects of the results.
Calculations with the full extensible theory [no # 0, d(r$’ + Or!) # 01 show only
flutter: for the quarter-circular pipe at Z:f E 2.9; for the semi-circular pipe at Zzf 2 0.99,
as shown in Figure 6.26 (Misra et al. 1988b). Thus, the predicted dynamical behaviour
is quite different.
In conclusion, it may be said that, despite several questions remaining unresolved, it is
clear that, if axial sliding is permitted, the system behaves in a manner reminiscent of a
curved cantilevered pipe: its eigenfrequencies are strongly dependent on the flow velocity
and the system eventually loses stability at high enough flow.
Incidentally, it is also observed that the variation of the first-mode frequency with flow
in Figure 6.25 (and similar ones for other 0) as predicted by the modified inextensible
theory and for ii* 5 2.8 in Figure 6.26 is qualitatively similar to that of the conventional
inextensible theory for clamped-clamped pipes. This offers a plausible explanation as to
why the dynamics of slightly curved pipes in the experiments by Liu & Mote (1974)
paradoxically appears to be in better agreement with conventional inextensible than with
extensible theory [see Figure 3.26 and Doll & Mote (1976)l: in both theories axial sliding