Page 545 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

NONLINEAR DYNAMICS THEORY APPLIED TO A PIPE CONVEYING FLUID 5 15

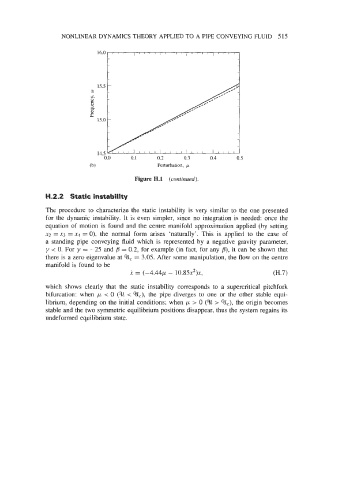
(b) Perturbation, p
Figure H.l (continued).

H.2.2 Static instability
The procedure to characterize the static instability is very similar to the one presented
for the dynamic instability. It is even simpler, since no integration is needed: once the
equation of motion is found and the centre manifold approximation applied (by setting
x:! = x3 = x4 = 0), the normal form arises 'naturally'. This is applied to the case of
a standing pipe conveying fluid which is represented by a negative gravity parameter,
y < 0. For y = -25 and B = 0.2, for example (in fact, for any B), it can be shown that
there is a zero eigenvalue at QC = 3.05. After some manipulation, the flow on the centre
manifold is found to be
X = (-4.44~ - 1O.85x2)x, (H.7)

which shows clearly that the static instability corresponds to a supercritical pitchfork
bifurcation: when p < 0 ("11 < QC), the pipe diverges to one or the other stable equi-
librium, depending on the initial conditions; when p > 0 ("11 > QC), the origin becomes
stable and the two symmetric equilibrium positions disappear, thus the system regains its
undeformed equilibrium state.