Page 549 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

THE FRACTAL DIMENSION FROM THE EXPERIMENTAL PIPE-VIBRATION 5 19

1 .0

- 0 0.5
g -20 -
E 2 0.0
g 40
-
e
-0.5
% -60
v)
-80 -1.0
0 5 10 15 20 25 0 1 2 3 4 5
Frequency (Hz) J
(a) (b)

0
-
E:
+
- -6
E
-8
400 -10
400 600 -7 -6 -5 4 -3 -2 -1 0

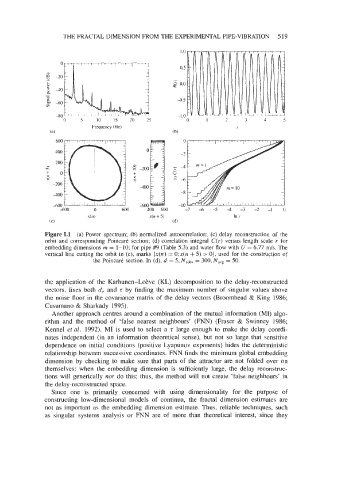
Figure 1.1 (a) Power spectrum; (b) normalized autocorrelation; (c) delay reconstruction of the
orbit and corresponding PoincarC section; (d) correlation integral C(r) versus length scale r for
embedding dimensions rn = 1 - 10; for pipe #9 (Table 5.3) and water flow with U = 6.77 ds. The
vertical line cutting the orbit in (c), marks (x(n) = O;x(n + 5) > 0}, used for the construction of
the PoincarC section. In (d), d = 5, Nsubs = 300, N,, = 50.

the application of the Karhunen-Lo&ve (KL) decomposition to the delay-reconstructed
vectors, fixes both de and t by finding the maximum number of singular values above
the noise floor in the covariance matrix of the delay vectors (Broomhead & King 1986;
Cusumano & Sharkady 1995).
Another approach centres around a combination of the mutual information (MI) algo-
rithm and the method of ‘false nearest neighbours’ (FNN) (Fraser & Swinney 1986;
Kennel et al. 1992). MI is used to select a t large enough to make the delay coordi-
nates independent (in an information theoretical sense), but not so large that sensitive
dependence on initial conditions (positive Lyapunov exponents) hides the deterministic
relationship between successive coordinates. FNN finds the minimum global embedding
dimension by checking to make sure that parts of the attractor are not folded over on
themselves: when the embedding dimension is sufficiently large, the delay reconstruc-
tions will generically not do this; thus, the method will not create ‘false neighbours’ in
the delay-reconstructed space.
Since one is primarily concerned with using dimensionality for the purpose of
constructing low-dimensional models of continua, the fractal dimension estimates are
not as important as the embedding dimension estimate. Thus, reliable techniques, such
as singular systems analysis or FNN are of more than theoretical interest, since they