Page 74 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)
P. 74
CONCEPTS, DEFINITIONS AND METHODS 57
Figure 2.13, as it stands, serves also to introduce the concept of coexisting amactors
(the stable fixed points and limit cycles), each with its own basin ofattraction: i.e. the
part of phase space within which trajectories are attracted, as if by a magnet, to this or
that state or attractor. The trajectories leading to and emanating from the saddle point
(thus tracing an x-intersection) are referred to as separatrices. In this case they separate
the basins of attraction of the stable limit cycle around {0, O} from those about {&15, O}.
A final point in this regard is the evolution and mutual interference of attractors. Let
us say that, as v' is varied, the coefficients in (2.166) are altered accordingly, and the
equation of motion for another U becomes
ji + 0.02 (1 - 1 Mi2 + 0.0625X4) X
+ (1 - 4.444 10-2~2 + 1.778 io-4~) = 0. (2.167)
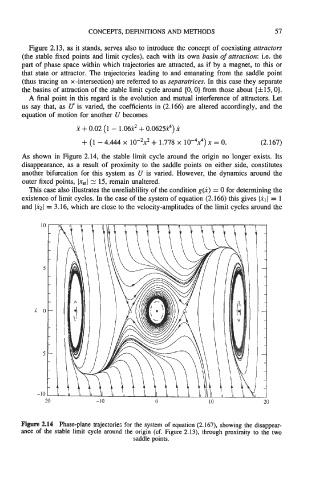
As shown in Figure 2.14, the stable limit cycle around the origin no longer exists. Its
disappearance, as a result of proximity to the saddle points on either side, constitutes
another bifurcation for this system as U is varied. However, the dynamics around the
outer fixed points, lxstl E 15, remain unaltered.
This case also illustrates the unreliablility of the condition g(X) = 0 for determining the
existence of limit cycles. In the case of the system of equation (2.166) this gives 1x1 I = 1
and 1x21 = 3.16, which are close to the velocity-amplitudes of the limit cycles around the
I
t L
-10 0 10
Figure 2.14 Phase-plane trajectories for the system of equation (2.167), showing the disappear-
ance of the stable limit cycle around the origin (cf. Figure 2.13), through proximity to the two
saddle points.