Page 107 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

PIPES CONVEYING FLUID: LINEAR DYNAMICS I 89

- f8 1st and 2nd modes -

1 I I I I I I

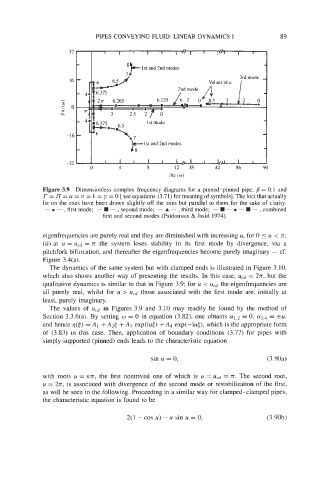
Figure 3.9 Dimensionless complex frequency diagrams for a pinned-pinned pipe; ,9 = 0.1 and
r = 17 = (II = cr = k = y = 0 [ see equations (3.71) for meaning of symbols]. The loci that actually
lie on the axes have been drawn slightly off the axes but parallel to them for the sake of clarity.
- - , first mode; - W - , second mode; - A - , third mode; - W - - W - , combined
0
first and second modes (Paldoussis & Issid 1974).

eigenfrequencies are purely real and they are diminished with increasing u, for 0 5 u < n;
(ii) at u = U,d = n the system loses stability in its first mode by divergence, via a
pitchfork bifurcation, and thereafter the eigenfrequencies become purely imaginary - cf.
Figure 3.4(a).
The dynamics of the same system but with clamped ends is illustrated in Figure 3.10,
which also shows another way of presenting the results. In this case, U,d = 217, but the
qualitative dynamics is similar to that in Figure 3.9; for u < U,d the eigenfrequencies are
all purely real, whilst for u > U,d those associated with the first mode are, initially at
least, purely imaginary.
The values of U,d in Figures 3.9 and 3.10 may readily be found by the method of
Section 3.3.6(a). By setting w = 0 in equation (3.82), one obtains a1,2 = 0, a3,4 = *tu,
and hence q(c) = AI + A26 + A3 exp(iuc) + A4 exp(-iuc), which is the appropriate form
of (3.83) in this case. Then, application of boundary conditions (3.77) for pipes with
simply-supported (pinned) ends leads to the characteristic equation

sin u = 0, (3.90a)

with roots u = nn, the first nontrivial one of which is u = u,d = n. The second root,
u = 275, is associated with divergence of the second mode or restabilization of the first,
as will be seen in the following. Proceeding in a similar way for clamped-clamped pipes,
the characteristic equation is found to be

2(1 - cos u) - u sin u = 0, (3.90b)