Page 108 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

90 SLENDER STRUCTURES AND AXIAL FLOW

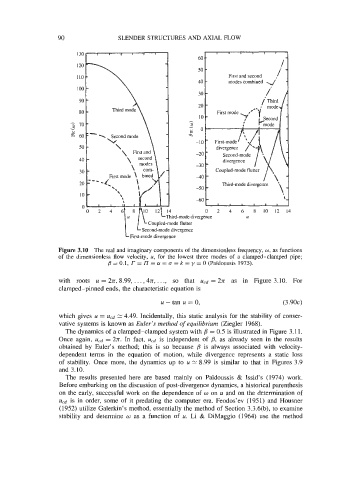
Figure 3.10 The real and imaginary components of the dimensionless frequency, w, as functions
of the dimensionless flow velocity, u, for the lowest three modes of a clamped-clamped pipe;
#? = 0.1, r = l7 = a = u = k = y = 0 (Pai’doussis 1975).

with roots u = 2n, 8.99, . . . ,4n, . . ., so that Ucd = 2n as in Figure 3.10. For
clamped-pinned ends, the characteristic equation is
u - tan u = 0, (3.90~)

which gives u = u,d 2 4.49. Incidentally, this static analysis for the stability of conser-
vative systems is known as Euler’s method of equilibrium (Ziegler 1968).
The dynamics of a clamped-clamped system with 6 = 0.5 is illustrated in Figure 3.1 1.
Once again, u,d = 2n. In fact, u,d is independent of 6, as already seen in the results
obtained by Euler’s method; this is so because j3 is always associated with velocity-
dependent terms in the equation of motion, while divergence represents a static loss
of stability. Once more, the dynamics up to u 2: 8.99 is similar to that in Figures 3.9
and 3.10.
The results presented here are based mainly on Pdidoussis & Issid’s (1974) work.
Before embarking on the discussion of post-divergence dynamics, a historical parenthesis
on the early, successful work on the dependence of w on u and on the determination of
Ucd is in order, some of it predating the computer era. Feodos’ev (1951) and Housner
(1952) utilize Galerkin’s method, essentially the method of Section 3.3.6(b), to examine
stability and determine w as a function of u. Li & DiMaggio (1964) use the method