Page 113 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)
P. 113
PIPES CONVEYING FLUID: LINEAR DYNAMICS I 95
It should be pointed out that the term 2B1/2ub21 played an important role in all of
the foregoing, not accidentally but because it is associated with the Coriolis term in the
equation of motion, which in turn is what makes the system gyroscopic conservative,
rather than just conservative. It is of interest that calculations with /3 = 0 show that, when
the system is purely conservative, the only form of instability is divergence; coupled-mode
flutter does not arise.
Another effect of the Coriolis forces - despite not doing any net work over a cycle
of oscillation - is that they render classical normal modes impossible.' Thus, the modal
displacement patterns contain both stationary and travelling-wave components, as seen in
Figure 3.13(b,c). Physically, this is a consequence of the forward and backward travelling
waves having different phase speeds (Chen & Rosenberg 1971) - see also Section 3.7.
Contrast this to Figure 3.13(a), where u = 0 and the Coriolis forces vanish; in this case
classical normal modes do exist.
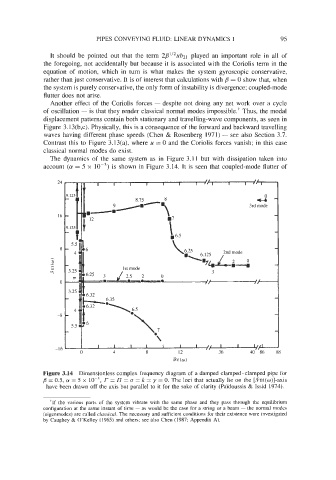
The dynamics of the same system as in Figure 3.1 1 but with dissipation taken into
account (a = 5 x lop3) is shown in Figure 3.14. It is seen that coupled-mode flutter of
24
16
8
0
-8
-16
0 4 8 12 36 40 86 88
%Sle (w)
Figure 3.14 Dimensionless complex frequency diagram of a damped clamped-clamped pipe for
j? = 0.5, a = 5 x IO-', r = I7 = o = k = y = 0. The loci that actually lie on the [9m(w)]-axis
have been drawn off the axis but parallel to it for the sake of clarity (Pai'doussis & Issid 1974).
'If the various parts of the system vibrate with the same phase and they pass through the equilibrium
configuration at the same instant of time - as would be the case for a string or a beam - the normal modes
(eigenmodes) are called classical. The necessary and sufficient conditions for their existence were investigated
by Caughey & O'Kelley (1965) and others: see also Chen (1987; Appendix A).