Page 109 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

PIPES CONVEYING FLUID: LINEAR DYNAMICS I 91

I 1 I 1-1 I p- I '-/ r
I
I
16 - -
- .q0 -
'-; 8.5 d5 Combined 1st and 2nd modes
8- , -
- 6.5, I' ' 3rd mode
e 8.96 -
9
3 -- 9.1 - 2nd mode 2J0
z 0' - -pzy/ A
..
2.rr"' :.28 6 . 6 2 7 T-- -
0
I st mode
19.5 -
8
-8 6.5f: \ -
\ 10
-16 - -
,\& ,,
I I -/ ' J
0 4 16 20
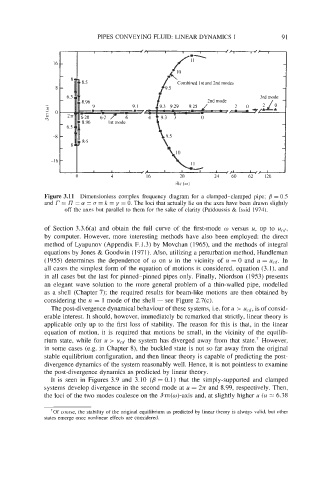
Figure 3.11 Dimensionless complex frequency diagram for a clamped-clamped pipe; = 0.5
and r = l7 = a! = (r = k = y = 0. The loci that actually lie on the axes have been drawn slightly
off the axes but parallel to them for the sake of clarity (Pai'doussis & Issid 1974).

of Section 3.3.6(a) and obtain the full curve of the first-mode o versus u, up to uCd,
by computer. However, more interesting methods have also been employed: the direct
method of Lyapunov (Appendix F.1.3) by Movchan (1965), and the methods of integral
equations by Jones & Goodwin (1 97 1). Also, utilizing a perturbation method, Handleman
(1955) determines the dependence of w on u in the vicinity of u = 0 and u = ucd. In
all cases the simplest form of the equation of motions is considered, equation (3.1), and
in all cases but the last for pinned-pinned pipes only. Finally, Niordson (1953) presents
an elegant wave solution to the more general problem of a thin-walled pipe, modelled
as a shell (Chapter 7); the required results for beam-like motions are then obtained by
considering the n = 1 mode of the shell - see Figure 2.7(c).
The post-divergence dynamical behaviour of these systems, i.e. for u > U,d, is of consid-
erable interest. It should, however, immediately be remarked that strictly, linear theory is
applicable only up to the first loss of stability. The reason for this is that, in the linear
equation of motion, it is required that motions be small, in the vicinity of the equilib-
rium state, while for u > u,d the system has diverged away from that state.' However,
in some cases (e.g. in Chapter S), the buckled state is not so far away from the original
stable equilibrium configuration, and then linear theory is capable of predicting the post-
divergence dynamics of the system reasonably well. Hence, it is not pointless to examine
the post-divergence dynamics as predicted by linear theory.
It is seen in Figures 3.9 and 3.10 (,!? = 0.1) that the simply-supported and clamped
systems develop divergence in the second mode at u = 2n and 8.99, respectively. Then,
the loci of the two modes coalesce on the Sm(w)-axis and, at slightly higher u (u 2 6.38

'Of course, the stability of the original equilibrium as predicted by linear theory is always valid, but other
states emerge once nonlinear effects are considered.