Page 111 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

PIPES CONVEYING FLUID: LINEAR DYNAMICS I 93

u -
8- Divergence

1
Stable

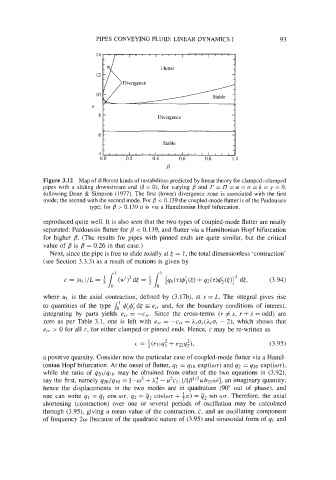
Figure 3.12 Map of different kinds of instabilities predicted by linear theory for clamped-clamped
pipes with a sliding downstream end (6 = O), for varying p and r = 17 = CY = o = k = y = 0,
following Done & Simpson (1977). The first (lower) divergence zone is associated with the first
mode; the second with the second mode. For p < 0.139 the coupled-mode flutter is of the Pai'doussis
type; for p > 0.139 it is via a Hamiltonian Hopf bifurcation.

reproduced quite well. It is also seen that the two types of coupled-mode flutter are neatly
separated: PaTdoussis flutter for 6 < 0.139, and flutter via a Hamiltonian Hopf bifurcation
for higher 6. (The results for pipes with pinned ends are quite similar, but the critical
value of is = 0.26 in that case.)
Next, since the pipe is free to slide axially at 6 = 1, the total dimensionless 'contraction'
(see Section 3.3.3) as a result of motions is given by
I' I'
c = IuLI/L = 3 (W'l2d6 = 3 [qi(t)4;(6> + 42(t)41(t)I2 dt7 (3.94)

where UL is the axial contraction, defined by (3.17b), at s = L. The integral gives rise
to quantities of the type IO @#; d6 esr and, for the boundary conditions of interest,
1
integrating by parts yields esr = -csr. Since the cross-terns (r # s, r + s = odd) are
zero as per Table 3.1, one is left with err = -crr = hror(krcr - 2), which shows that
err > 0 for all r, for either clamped or pinned ends. Hence, c may be re-written as

2
2
c = ;(ellql +e22q2), (3.95)
a positive quantity. Consider now the particular case of coupled-mode flutter via a Hamil-
tonian Hopf bifurcation. At the onset of flutter, q1 = 410 exp(iwt) and q2 = q20 exp(iwt),
while the ratio of q20/ql0 may be obtained from either of the two equations in (3.92),
say the first, namely q20/q10 = [-w2 + h;' - ~~ql]/[~'/~~b21wi], an imaginary quantity;
hence the displacements in the two modes are in quadrature (90" out of phase), and
one can write ql = q1 cos wr, q2 = q2 cos(ot + ix) = q2 sin or. Therefore, the axial
shortening (contraction) over one or several periods of oscillation may be calculated
through (3.95), giving a mean value of the contraction, C, and an oscillating component
of frequency 2w [because of the quadratic nature of (3.95) and sinusoidal form of ql and