Page 207 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

PIPES CONVEYING FLUID: LINEAR DYNAMICS I 189

cases, however, it is the locus of the mode giving rise to flutter that reaches the negative
4m(w)-axis and then crosses the origin from instability to stability; these cases are shown
as dashed lines for N = 2 and 4 and low y. This appears to be the usual path for N
odd. although for N = 5 and 7, over a range of y, the mode locus recrosses to instability
(the upper curve in each case). However, for N = 5 and large or small enough y, there
are no crossings of the origin at all, thus leading to the finite closed curve shown in the
figure; for N = 3 the area of this closed curve is simply null. Thus, in this respect also,
the transition from N = 3 to higher odd values of N may be considered to be ‘smooth’.
Experiments were also conducted, similar to those of Benjamin’s, with metal tubes
(diameter = 9.5- 12.7 mm, L 2: 0.6- 1.2 m), with connector-springs made of rubber tubing
secured by jubilee clips, N = 2, 3 or 4, and water as the fluid. In some cases, in order to
increase m and hence y, the tubes were sheathed with larger diameter tubes. Typical results
are given in Table 3.7. In all the cases in (a) stability is lost by flutter, while in (b) it
is lost by divergence. The experiments in (b) were conducted with springs of negligible
stiffness, in which case u and y, as defined in (3.163) are meaningless; in that case, a
new dimensionalization was made, in terms of the Froude number, F = U/(gL)’/2. For
N = 2, e = i, it is shown analytically that, for divergence, F = &d = 1/(28)’/2. As seen
in the table, agreement between theory and experiment is reasonably good in all cases.

2o

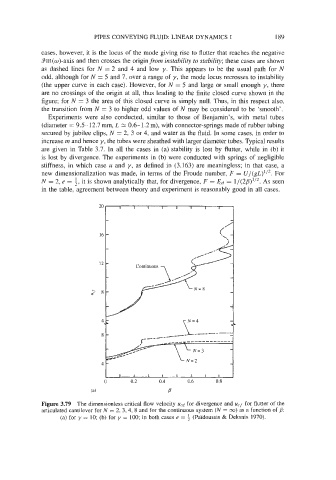
Figure 3.79 The dimensionless critical flow velocity Ucd for divergence and ucf for flutter of the
articulated cantilever for N = 2, 3,4,8 and for the continuous system (N = 00) as a function of B:
(a) for y = 10; (b) for y = 100; in both cases e = (Pafdoussis & Deksnis 1970).