Page 218 - T. Anderson-Fracture Mechanics - Fundamentals and Applns.-CRC (2005)

1656_C004.fm Page 198 Thursday, April 21, 2005 5:38 PM

198 Fracture Mechanics: Fundamentals and Applications

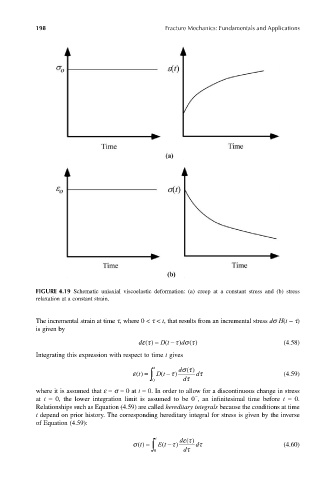
FIGURE 4.19 Schematic uniaxial viscoelastic deformation: (a) creep at a constant stress and (b) stress
relaxation at a constant strain.

The incremental strain at time τ, where 0 < τ < t, that results from an incremental stress dσ H(t − τ)
is given by
d Dετ () = t τ σ τ() (4.58)
d ( −
)
Integrating this expression with respect to time t gives

ε ∫ t D = ( − t τ() t ) d στ() τ d (4.59)
0 τ d
where it is assumed that ε = σ = 0 at t = 0. In order to allow for a discontinuous change in stress
−
at t = 0, the lower integration limit is assumed to be 0 , an infinitesimal time before t = 0.
Relationships such as Equation (4.59) are called hereditary integrals because the conditions at time
t depend on prior history. The corresponding hereditary integral for stress is given by the inverse
of Equation (4.59):

σ ∫ t ( E = t − τ() t ) d ετ() τ d (4.60)
0 τ d