Page 376 - T. Anderson-Fracture Mechanics - Fundamentals and Applns.-CRC (2005)

1656_C008.fm Page 356 Monday, May 23, 2005 5:59 PM

356 Fracture Mechanics: Fundamentals and Applications

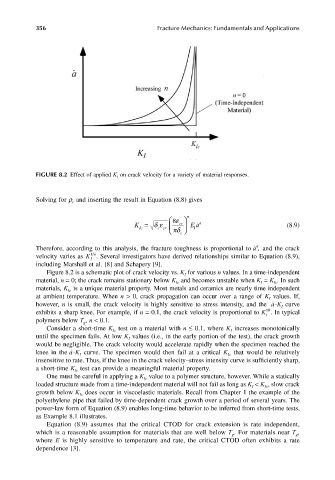
FIGURE 8.2 Effect of applied K I on crack velocity for a variety of material responses.

Solving for ρ and inserting the result in Equation (8.8) gives
c
 ε 8  n
K Ic c cr   πδ cr c   E 1 a= δε ˙ n (8.9)

Therefore, according to this analysis, the fracture toughness is proportional to ˙ ,a n and the crack
velocity varies as K 1/ n . Several investigators have derived relationships similar to Equation (8.9),
I
including Marshall et al. [8] and Schapery [9].
Figure 8.2 is a schematic plot of crack velocity vs. K for various n values. In a time-independent
I
material, n = 0; the crack remains stationary below K and becomes unstable when K = K . In such
Ic
I
Ic
materials, K is a unique material property. Most metals and ceramics are nearly time independent
Ic
at ambient temperature. When n > 0, crack propagation can occur over a range of K values. If,
I
˙ a
however, n is small, the crack velocity is highly sensitive to stress intensity, and the -K curve
I
10
exhibits a sharp knee. For example, if n = 0.1, the crack velocity is proportional to K . In typical
I
polymers below T , n < 0.1.
g
Consider a short-time K test on a material with n ≤ 0.1, where K increases monotonically
I
Ic
until the specimen fails. At low K values (i.e., in the early portion of the test), the crack growth
I
would be negligible. The crack velocity would accelerate rapidly when the specimen reached the
˙ a
knee in the -K curve. The specimen would then fail at a critical K that would be relatively
I
Ic
insensitive to rate. Thus, if the knee in the crack velocity–stress intensity curve is sufficiently sharp,
a short-time K test can provide a meaningful material property.
Ic
One must be careful in applying a K value to a polymer structure, however. While a statically
Ic
loaded structure made from a time-independent material will not fail as long as K < K , slow crack
I
Ic
growth below K does occur in viscoelastic materials. Recall from Chapter 1 the example of the
Ic
polyethylene pipe that failed by time-dependent crack growth over a period of several years. The
power-law form of Equation (8.9) enables long-time behavior to be inferred from short-time tests,
as Example 8.1 illustrates.
Equation (8.9) assumes that the critical CTOD for crack extension is rate independent,
which is a reasonable assumption for materials that are well below T . For materials near T ,
g
g
where E is highly sensitive to temperature and rate, the critical CTOD often exhibits a rate
dependence [3].