Page 378 - T. Anderson-Fracture Mechanics - Fundamentals and Applns.-CRC (2005)

1656_C008.fm Page 358 Monday, May 23, 2005 5:59 PM

358 Fracture Mechanics: Fundamentals and Applications

(a)

(b)

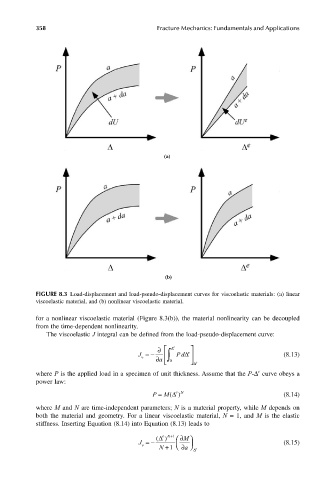
FIGURE 8.3 Load-displacement and load-pseudo-displacement curves for viscoelastic materials: (a) linear
viscoelastic material, and (b) nonlinear viscoelastic material.

for a nonlinear viscoelastic material (Figure 8.3(b)), the material nonlinearity can be decoupled
from the time-dependent nonlinearity.
The viscoelastic J integral can be defined from the load-pseudo-displacement curve:
∂  ∆ e 
e
J =−  ∫ Pd  (8.13)
∆
a ∂
v
  0 ∆ e  
e
where P is the applied load in a specimen of unit thickness. Assume that the P-∆ curve obeys a
power law:
e N
P M = () (8.14)
∆
where M and N are time-independent parameters; N is a material property, while M depends on
both the material and geometry. For a linear viscoelastic material, N = 1, and M is the elastic
stiffness. Inserting Equation (8.14) into Equation (8.13) leads to
∆
e N+1
J =− ()   ∂ M   (8.15)
v
N +1  a ∂  ∆ e