Page 423 - T. Anderson-Fracture Mechanics - Fundamentals and Applns.-CRC (2005)

1656_C009.fm Page 403 Monday, May 23, 2005 3:58 PM

Application to Structures 403

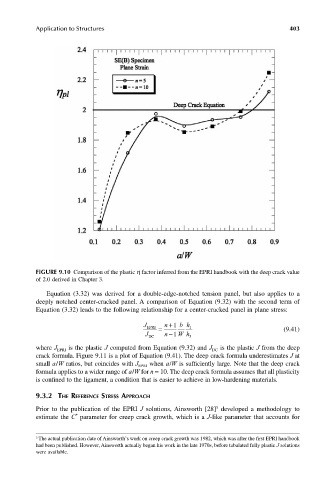
FIGURE 9.10 Comparison of the plastic h factor inferred from the EPRI handbook with the deep crack value
of 2.0 derived in Chapter 3.

Equation (3.32) was derived for a double-edge-notched tension panel, but also applies to a
deeply notched center-cracked panel. A comparison of Equation (9.32) with the second term of
Equation (3.32) leads to the following relationship for a center-cracked panel in plane stress:
J EPRI = n +1 b h 1
J n −1 W h (9.41)
DC 3
where J EPRI is the plastic J computed from Equation (9.32) and J is the plastic J from the deep
DC
crack formula. Figure 9.11 is a plot of Equation (9.41). The deep crack formula underestimates J at
small a/W ratios, but coincides with J EPRI when a/W is sufficiently large. Note that the deep crack
formula applies to a wider range of a/W for n = 10. The deep crack formula assumes that all plasticity
is confined to the ligament, a condition that is easier to achieve in low-hardening materials.

9.3.2 THE REFERENCE STRESS APPROACH

3
Prior to the publication of the EPRI J solutions, Ainsworth [28] developed a methodology to
*
estimate the C parameter for creep crack growth, which is a J-like parameter that accounts for
3 The actual publication date of Ainsworth’s work on creep crack growth was 1982, which was after the first EPRI handbook
had been published. However, Ainsworth actually began his work in the late 1970s, before tabulated fully plastic J solutions
were available.