Page 424 - T. Anderson-Fracture Mechanics - Fundamentals and Applns.-CRC (2005)

1656_C009.fm Page 404 Monday, May 23, 2005 3:58 PM

404 Fracture Mechanics: Fundamentals and Applications

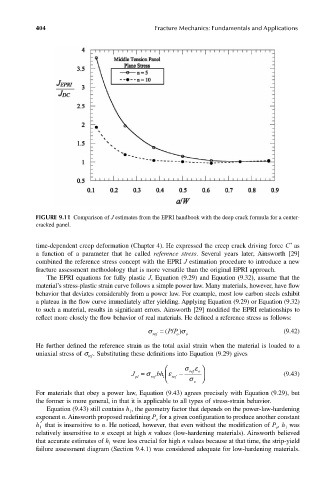
FIGURE 9.11 Comparison of J estimates from the EPRI handbook with the deep crack formula for a center-
cracked panel.

*
time-dependent creep deformation (Chapter 4). He expressed the creep crack driving force C as
a function of a parameter that he called reference stress. Several years later, Ainsworth [29]
combined the reference stress concept with the EPRI J estimation procedure to introduce a new
fracture assessment methodology that is more versatile than the original EPRI approach.
The EPRI equations for fully plastic J, Equation (9.29) and Equation (9.32), assume that the
material’s stress-plastic strain curve follows a simple power law. Many materials, however, have flow
behavior that deviates considerably from a power law. For example, most low carbon steels exhibit
a plateau in the flow curve immediately after yielding. Applying Equation (9.29) or Equation (9.32)
to such a material, results in significant errors. Ainsworth [29] modified the EPRI relationships to
reflect more closely the flow behavior of real materials. He defined a reference stress as follows:
σ ref = (/ o σ o (9.42)
PP )
He further defined the reference strain as the total axial strain when the material is loaded to a
uniaxial stress of s . Substituting these definitions into Equation (9.29) gives
ref
 σε 
J b = h  ε − σ ref o  (9.43)
pl
ref
 ref σ o 
1
For materials that obey a power law, Equation (9.43) agrees precisely with Equation (9.29), but
the former is more general, in that it is applicable to all types of stress-strain behavior.
Equation (9.43) still contains h , the geometry factor that depends on the power-law-hardening
1
exponent n. Ainsworth proposed redefining P for a given configuration to produce another constant
o
h ′ that is insensitive to n. He noticed, however, that even without the modification of P , h was
o
1
1
relatively insensitive to n except at high n values (low-hardening materials). Ainsworth believed
that accurate estimates of h were less crucial for high n values because at that time, the strip-yield
1
failure assessment diagram (Section 9.4.1) was considered adequate for low-hardening materials.