Page 69 - T. Anderson-Fracture Mechanics - Fundamentals and Applns.-CRC (2005)
P. 69
1656_C02.fm Page 49 Thursday, April 14, 2005 6:28 PM
Linear Elastic Fracture Mechanics 49
π a
K = λσ Q f φ()
s
I
π a . 165
K = σ Q f φ() Q =+ . 1 464 a
I
1
c
a
φ
λ s = . − 113 009 c [1 01 − . (1 sin ) ]
+
2
.
a 2 / 14
φ
f φ = 2 φ ( ) + sin ( ) cos ( )
2
c
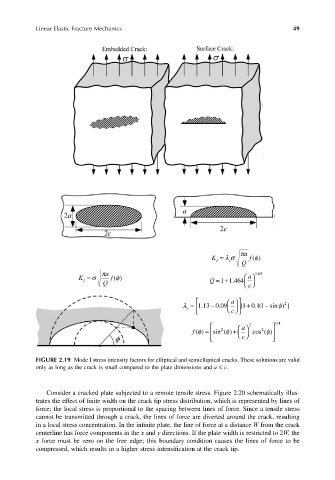
FIGURE 2.19 Mode I stress intensity factors for elliptical and semielliptical cracks. These solutions are valid
only as long as the crack is small compared to the plate dimensions and a ≤ c.
Consider a cracked plate subjected to a remote tensile stress. Figure 2.20 schematically illus-
trates the effect of finite width on the crack tip stress distribution, which is represented by lines of
force; the local stress is proportional to the spacing between lines of force. Since a tensile stress
cannot be transmitted through a crack, the lines of force are diverted around the crack, resulting
in a local stress concentration. In the infinite plate, the line of force at a distance W from the crack
centerline has force components in the x and y directions. If the plate width is restricted to 2W, the
x force must be zero on the free edge; this boundary condition causes the lines of force to be
compressed, which results in a higher stress intensification at the crack tip.