Page 68 - T. Anderson-Fracture Mechanics - Fundamentals and Applns.-CRC (2005)

1656_C02.fm Page 48 Thursday, April 14, 2005 6:28 PM

48 Fracture Mechanics: Fundamentals and Applications

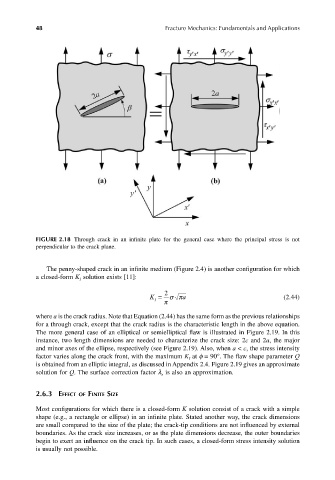
FIGURE 2.18 Through crack in an infinite plate for the general case where the principal stress is not
perpendicular to the crack plane.

The penny-shaped crack in an infinite medium (Figure 2.4) is another configuration for which
a closed-form K solution exists [11]:
I
2
K I π σπ a = (2.44)

where a is the crack radius. Note that Equation (2.44) has the same form as the previous relationships
for a through crack, except that the crack radius is the characteristic length in the above equation.
The more general case of an elliptical or semielliptical flaw is illustrated in Figure 2.19. In this
instance, two length dimensions are needed to characterize the crack size: 2c and 2a, the major
and minor axes of the ellipse, respectively (see Figure 2.19). Also, when a < c, the stress intensity
factor varies along the crack front, with the maximum K at φ = 90°. The flaw shape parameter Q
I
is obtained from an elliptic integral, as discussed in Appendix 2.4. Figure 2.19 gives an approximate
solution for Q. The surface correction factor λ is also an approximation.
s

2.6.3 EFFECT OF FINITE SIZE

Most configurations for which there is a closed-form K solution consist of a crack with a simple
shape (e.g., a rectangle or ellipse) in an infinite plate. Stated another way, the crack dimensions
are small compared to the size of the plate; the crack-tip conditions are not influenced by external
boundaries. As the crack size increases, or as the plate dimensions decrease, the outer boundaries
begin to exert an influence on the crack tip. In such cases, a closed-form stress intensity solution
is usually not possible.