Page 313 - Fundamentals of Gas Shale Reservoirs

RESERVOIR MODELING AND SIMULATION 293
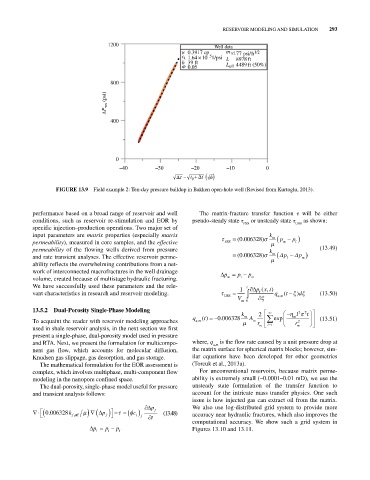
1200 Well data
0.3917 cp m 1/2 77 psi/h 1/2
c t 1.64×10 1/psi L 8978ft
–5
h 39 ft 4489ft (50%)
0.05 L eff
800

P ws (psi)

400

0
–40 –30 –20 –10 0
–
√ t √ t p + t (√ h)
FIgURE 13.9 Field example 2: Ten‐day pressure buildup in Bakken open‐hole well (Revised from Kurtoglu, 2013).

performance based on a broad range of reservoir and well The matrix‐fracture transfer function τ will be either
conditions, such as reservoir re‐stimulation and EOR by pseudo‐steady state τ or unsteady state τ USS as shown:
PSS
specific injection–production operations. Two major set of
input parameters are matrix properties (especially matrix k m
0
permeability), measured in core samples, and the effective PSS (.006328 ) p m p f
permeability of the flowing wells derived from pressure k (13.49)
0
and rate transient analyses. The effective reservoir perme- (.006328 ) m p f p m
ability reflects the overwhelming contributions from a net-
work of interconnected macrofractures in the well drainage p p p
volume, created because of multistage hydraulic fracturing. m i m
We have successfully used these parameters and the rele- 1 t px ( , t)
vant characteristics in research and reservoir modeling. f q t ( d ) (13.50)
USS V um
,
m 0
13.5.2 Dual-Porosity Single-Phase Modeling 2 2
q t () . 0 006328 k m A 2 exp m l t (13.51)
To acquaint the reader with reservoir modeling approaches um m r r 2
,
used in shale reservoir analysis, in the next section we first m l 1 m
present a single‐phase, dual‐porosity model used in pressure
and RTA. Next, we present the formulation for multicompo- where, q is the flow rate caused by a unit pressure drop at
u,m
nent gas flow, which accounts for molecular diffusion, the matrix surface for spherical matrix blocks; however, sim-
Knudsen gas slippage, gas desorption, and gas storage. ilar equations have been developed for other geometries
The mathematical formulation for the EOR assessment is (Torcuk et al., 2013a).
complex, which involves multiphase, multi‐component flow For unconventional reservoirs, because matrix perme-
modeling in the nanopore confined space. ability is extremely small (~0.0001–0.01 mD), we use the
The dual‐porosity, single‐phase model useful for pressure unsteady state formulation of the transfer function to
and transient analysis follows: account for the intricate mass transfer physics. One such
issue is how injected gas can extract oil from the matrix.
p We also use log‐distributed grid system to provide more
.
0 006328k p c f (13.48)
f ,eff f t f t accuracy near hydraulic fractures, which also improves the
computational accuracy. We show such a grid system in
p p p Figures 13.10 and 13.11.
f i f