Page 129 - Fundamentals of Ocean Renewable Energy Generating Electricity From The Sea

120 Fundamentals of Ocean Renewable Energy

kH b /2 = γ/2 and γ/2 ≈ 0.44−0.55 (5.43)
H b γ
→ = ≈ 0.14−0.17 (5.44)
L 2π
which is consistent with what we see in Fig. 5.4, and simply indicates that the
wave steepness (i.e. kH/2or H/L depending how it is defined) cannot go beyond
a threshold; see other resources for more details about this limit [8].

Nonlinear Dispersion Equation
As we discussed, the linear dispersion equation relates the water depth and the
wave frequency to the wave celerity (or wave length). If nonlinear effects are
considered, the dispersion equation will also be dependent on the wave height.
The nonlinear dispersion equation is given by [9]

2
H 2 8 + cosh 4kd − 2 tanh kd
2
σ = gk tanh kd 1 + k (5.45)
4
2 8 sinh kd
As can be seen, when kH/2 or the wave steepness is small, the previous
equation approaches what we already saw in the linear wave theory (Eq. 5.13).
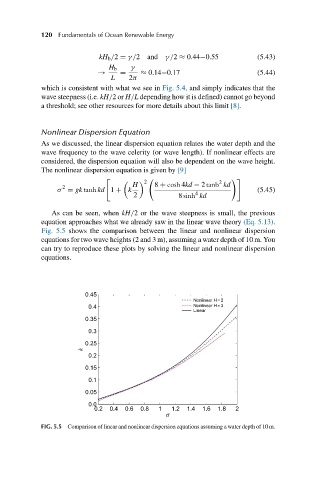
Fig. 5.5 shows the comparison between the linear and nonlinear dispersion
equations for two wave heights (2 and 3 m), assuming a water depth of 10 m. You
can try to reproduce these plots by solving the linear and nonlinear dispersion
equations.

0.45
Nonlinear H=2
0.4 Nonlinear H=3
Linear
0.35
0.3

0.25
k
0.2
0.15
0.1
0.05
0.0
0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
s
FIG. 5.5 Comparison of linear and nonlinear dispersion equations assuming a water depth of 10 m.